
【题目】某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照![]() 、
、![]() 、…、
、…、![]() 从少到多分成9组,制成样本的频率分布直方图如图所示.
从少到多分成9组,制成样本的频率分布直方图如图所示.
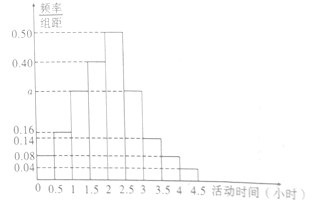
(1)求图中![]() 的值;
的值;
(2)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;
(3)在![]() 、
、![]() 这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]()
【解析】试题分析:(1)根据频率分布直方图计算![]() 的值;(2)根据频率分布直方图估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;(3)由题意得平均户外活动时间在
的值;(2)根据频率分布直方图估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;(3)由题意得平均户外活动时间在![]() ,
, ![]() 中的人数分别有15人、20人,按分层抽样的方法分别抽取3人、4人,记作A,B,C及a,b,c,d,从7人中随机抽取2人,共有21种,同时在同一组的有9种,从而得到抽取的两人恰好都在同一个组的概率.
中的人数分别有15人、20人,按分层抽样的方法分别抽取3人、4人,记作A,B,C及a,b,c,d,从7人中随机抽取2人,共有21种,同时在同一组的有9种,从而得到抽取的两人恰好都在同一个组的概率.
试题解析:
(Ⅰ)由频率分布直方图,可知,
平均户外“活动时间”在![]() 的频率为
的频率为![]() .
.
同理,在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 等组的频率分别为0.08,0.20,0.25,0.07,0.04,0.02,
等组的频率分别为0.08,0.20,0.25,0.07,0.04,0.02,
由![]() .
.
解得![]() .
.
(Ⅱ)设中位数为m小时.
因为前5组的频率之和为![]() ,
,
而前4组的频率之和为![]() ,所以
,所以![]() .
.
由![]() ,解得
,解得![]() .
.
故可估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数为2.06小时.
(Ⅲ)由题意得平均户外活动时间在![]() ,
, ![]() 中的人数分别有15人、20人,按分层抽样的方法分别抽取3人、4人,记作A,B,C及a,b,c,d,从7人中随机抽取2人,共有
中的人数分别有15人、20人,按分层抽样的方法分别抽取3人、4人,记作A,B,C及a,b,c,d,从7人中随机抽取2人,共有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .共21种,同时在同一组的有
.共21种,同时在同一组的有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .共9种,
.共9种,
故其概率是![]() .
.


科目:高中数学 来源: 题型:
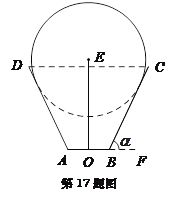
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列
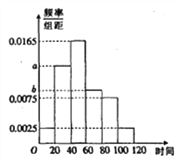
(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解城市交通压力,某市市政府在市区一主要交通干道修建高架桥,两端的桥墩现已建好,已知这两桥墩相距m米,“余下的工程”只需建两端桥墩之间的桥面和桥墩.经测算,一个桥墩的工程费用为256万元;距离为x米的相邻两墩之间的桥面工程费用为(2+![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记“余下工程”的费用为y万元.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素.记“余下工程”的费用为y万元.
(1)试写出工程费用y关于x的函数关系式;
(2)当m=640米时,需新建多少个桥墩才能使工程费用y最小?并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com