练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)=In(1+x)-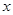+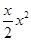(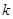≥0)。

    (1)当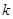=2时，求曲线y=f(x)在点(1，f(1))处的切线方程；

    (2)求函数f(x)的单调区间。

     

    【答案】

       

    所以的单调递增区间为，单调递减区间为；

    当时，，得;

    因此，在区间和上，；在区间上，；

    即函数 的单调递增区间为和，单调递减区间为；

    当时，.的递增区间为

    当时，由，得；

    因此，在区间和上，，在区间上，；

    即函数 的单调递增区间为和，单调递减区间为…………12分

     

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    x2+1x-1
    ，其图象在点（0，-1）处的切线为l．
    （I）求l的方程；
    （II）求与l平行的切线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    		3
    sinxcosx+cos2x+1    ．
    （I）求f（x）的最小正周期及单调递减区间；
    （II）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=2，b=1，△ABC的面积为
    		3
    2
    ，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=sin(x+
    π
    4
    )+2cos(x-
    π
    4
    )+2sin2x+3cos(x+
    3π
    4
    )    ；g(x)=f(x)+f2(
    x
    2
    )
    （I）求f(
    π
    4
    )    ；
    （II）求函数g（x）的最小正周期和单调递增区间；
    （III）在△ABC中，g（A）=4，
    AB
    AC
    =4
    		2
    ，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于函数 ，若存在，使  成立，则称为 的“滞点”.已知函数f ( x ) = .

    (I)试问有无“滞点”？若有，求之，否则说明理由；

    (II)已知数列的各项均为负数，且满足,求数列的通项公式；

    (III)已知,求的前项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (12 分)已知函数f(x)=.(I)求函数f(x)的定义域、值域；(II)若函数y=sin2x图象按向量＝(h,k)(|h|<)平移后可以得到函数f(x)的图象，求向量．

    查看答案和解析>>

    同步练习册答案