
【题目】已知函数![]() .
.
(1)求证:函数![]() 在
在![]() 内单调递增;
内单调递增;
(2)记![]() 为函数
为函数![]() 的反函数.若关于
的反函数.若关于![]() 的方程
的方程![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(3)若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD的底面为正方形,![]()
![]() ,AC与BD交于E,M,N分别为SD,SA的中点,
,AC与BD交于E,M,N分别为SD,SA的中点,![]() .
.
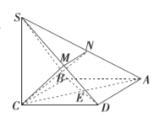
(1)求证:平面![]() 平面SBD;
平面SBD;
(2)求直线BD与平面CMN所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张,为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少0.5万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数量构成数列![]() ,每年发放电动型汽车牌照数为构成数列
,每年发放电动型汽车牌照数为构成数列![]() ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 由两个椭圆
由两个椭圆![]() :
:![]() 和椭圆
和椭圆![]() :
:![]() 组成,当
组成,当![]() 成等比数列时,称曲线
成等比数列时,称曲线![]() 为“猫眼曲线”.
为“猫眼曲线”.
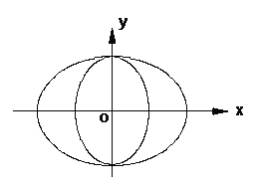
(1)若猫眼曲线![]() 过点
过点![]() ,且
,且![]() 的公比为
的公比为![]() ,求猫眼曲线
,求猫眼曲线![]() 的方程;
的方程;
(2)对于题(1)中的求猫眼曲线![]() ,任作斜率为
,任作斜率为![]() 且不过原点的直线与该曲线相交,交椭圆
且不过原点的直线与该曲线相交,交椭圆![]() 所得弦的中点为M,交椭圆
所得弦的中点为M,交椭圆![]() 所得弦的中点为N,求证:
所得弦的中点为N,求证:![]() 为与
为与![]() 无关的定值;
无关的定值;
(3)若斜率为![]() 的直线
的直线![]() 为椭圆
为椭圆![]() 的切线,且交椭圆
的切线,且交椭圆![]() 于点
于点![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点(点
上的任意一点(点![]() 与点
与点![]() 不重合),求
不重合),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设单调函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果单调函数
,如果单调函数![]() 使得函数
使得函数![]() 的值域也是
的值域也是![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的一个“保值域函数”.已知定义域为
的一个“保值域函数”.已知定义域为![]() 的函数
的函数![]() ,函数
,函数![]() 与
与![]() 互为反函数,且
互为反函数,且![]() 是
是![]() 的一个“保值域函数”,
的一个“保值域函数”,![]() 是
是![]() 的一个“保值域函数”,则
的一个“保值域函数”,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019年女排世界杯中,中国女子排球队以11连胜的优异战绩成功夺冠,为祖国母亲七十华诞献上了一份厚礼.排球比赛采用5局3胜制,前4局比赛采用25分制,每个队只有赢得至少25分,并同时超过对方2分时,才胜1局;在决胜局(第五局)采用15分制,每个队只有赢得至少15分,并领先对方2分为胜.在每局比赛中,发球方赢得此球后可得1分,并获得下一球的发球权,否则交换发球权,并且对方得1分.现有甲乙两队进行排球比赛:
(1)若前三局比赛中甲已经赢两局,乙赢一局.接下来两队赢得每局比赛的概率均为![]() ,求甲队最后赢得整场比赛的概率;
,求甲队最后赢得整场比赛的概率;
(2)若前四局比赛中甲、乙两队已经各赢两局比赛.在决胜局(第五局)中,两队当前的得分为甲、乙各14分,且甲已获得下一发球权.若甲发球时甲赢1分的概率为![]() ,乙发球时甲赢1分的概率为
,乙发球时甲赢1分的概率为![]() ,得分者获得下一个球的发球权.设两队打了
,得分者获得下一个球的发球权.设两队打了![]() 个球后甲赢得整场比赛,求x的取值及相应的概率p(x).
个球后甲赢得整场比赛,求x的取值及相应的概率p(x).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com