
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 是
是![]() 的中点.
的中点.
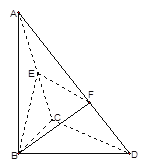
(Ⅰ)若![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
试题(Ⅰ)由![]() 平面
平面![]() 得
得![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() 平面
平面![]() ,又E、F分别是AC、AD的中点,所以
,又E、F分别是AC、AD的中点,所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;(Ⅱ)解法1:(坐标法)建立空间直角坐标系
;(Ⅱ)解法1:(坐标法)建立空间直角坐标系![]() ,写出相关点的坐标,解得平面
,写出相关点的坐标,解得平面![]() 的发向量
的发向量![]() ,而平面
,而平面![]() 的法向量是
的法向量是![]() =
=![]() ,通过空间向量的数量积运算求出法向量的夹角
,通过空间向量的数量积运算求出法向量的夹角![]() 的余弦为
的余弦为![]() ,所以锐二面角的大小为
,所以锐二面角的大小为![]() ;法2:(先作出二面角的平面角,再在三角形中求出角的大小).延长
;法2:(先作出二面角的平面角,再在三角形中求出角的大小).延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() , 过
, 过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() ,易证
,易证![]() 为所求二面角的平面角,在
为所求二面角的平面角,在![]() 中可求得
中可求得![]() ,在
,在![]() 中,可以解得
中,可以解得![]() ,所以在
,所以在![]() 中,
中,![]() ,即平面
,即平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.
试题解析:(Ⅰ)证明:![]() 平面
平面![]() ,
,![]() .
.
又![]() 平面
平面![]() .
.
![]() E、F分别是AC、AD的中点,
E、F分别是AC、AD的中点,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)解法1:如图建立空间直角坐标系![]() 则
则
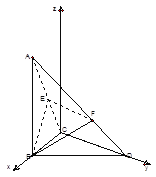
![]()
![]() ,
,![]()
![]() ,
,
设![]() 平面
平面![]() ,
,
则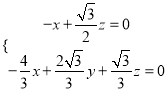 ,取
,取![]()
![]() 平面
平面![]() 的法向量是
的法向量是![]() =
=![]() ,
,
![]() , 所以,平面
, 所以,平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.
法2:延长![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连结
,连结![]() , 过
, 过![]() 作
作![]() 于
于![]()
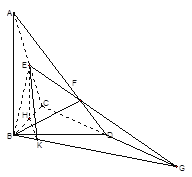
则![]() 平面
平面![]() ,
,
过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() ,
,
![]() 即为所求二面角的平面角.
即为所求二面角的平面角.
![]() ,
,
在![]() 中,可以解得
中,可以解得![]() ,
,
![]() 在
在![]() 中,
中,![]() ,即平面
,即平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为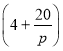 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 的对边,且满
的对边,且满![]() .
.
(1)求![]() 的大小;
的大小;
(2)再在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中,选出两个使
这三个条件中,选出两个使![]() 唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求
唯一确定的条件补充在下面的问题中,并解答问题.若________,________,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:

(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量![]() ,及松树数量
,及松树数量![]() 关于n的表达式
关于n的表达式
(2)定义:![]()
![]() 为
为![]() 增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省在2017年启动了“3+3”高考模式.所谓“3+3”高考模式,就是语文、数学、外语(简称语、数、外)为高考必考科目,从物理、化学、生物、政治、历史、地理(简称理、化、生、政、史、地)六门学科中任选三门作为选考科目.该省某中学2017级高一新生共有990人,学籍号的末四位数从0001到0990.
(1)现从高一学生中抽样调查110名学生的选考情况,问:采用什么样的抽样方法较为恰当?(只写出结论,不需要说明理由)
(2)据某教育机构统计,学生所选三门学科在将来报考专业时受限制的百分比是不同的.该机构统计了受限百分比较小的十二种选择的百分比值![]() ,制作出如下条形图.
,制作出如下条形图.
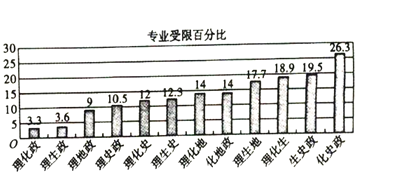
设以上条形图中受限百分比的均值为![]() ,标准差为
,标准差为![]() .如果一个学生所选三门学科专业受限百分比在区间
.如果一个学生所选三门学科专业受限百分比在区间![]() 内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?(均值
内,我们称该选择为“恰当选择”.该校李明同学选择了化学,然后从余下五门选考科目中任选两门.问李明的选择为“恰当选择"的概率是多少?(均值![]() ,标准差
,标准差![]() 均精确到0.1)
均精确到0.1)
(参考公式和数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是各项均为正数的等差数列,其公差
是各项均为正数的等差数列,其公差![]() 大于零.若线段
大于零.若线段![]() ,
,![]() ,
,![]() ,
,![]() 的长分别为
的长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( ).
,则( ).
A.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
B.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
C.对任意的![]() ,均存在以
,均存在以![]() ,
,![]() ,
,![]() 为三边的三角形
为三边的三角形
D.对任意的![]() ,均不存在以
,均不存在以![]() ,
,![]() ,
,为三边的三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
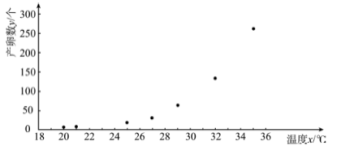
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com