
ЁОЬтФПЁПКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() МАДЫЪБ
МАДЫЪБ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ЁОД№АИЁП(1) 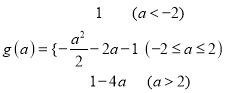 ЃЛ(2)Д№АИМћНтЮі.
ЃЛ(2)Д№АИМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУЭЌНЧШ§НЧКЏЪ§МфЕФЛљБОЙиЯЕЛЏМђКЏЪ§НтЮіЪНКѓЃЌЗжШ§жжЧщПіЃКЂй![]() аЁгкЉ1ЪБЂк
аЁгкЉ1ЪБЂк![]() ДѓгкЉ1ЖјаЁгк1ЪБЂл
ДѓгкЉ1ЖјаЁгк1ЪБЂл![]() Дѓгк1ЪБЃЌИљОнЖўДЮКЏЪ§ЧѓзюаЁжЕЕФЗНЗЈЧѓГіfЃЈxЃЉЕФзюаЁжЕgЃЈaЃЉЕФжЕМДПЩЃЛЃЈ2ЃЉАб
Дѓгк1ЪБЃЌИљОнЖўДЮКЏЪ§ЧѓзюаЁжЕЕФЗНЗЈЧѓГіfЃЈxЃЉЕФзюаЁжЕgЃЈaЃЉЕФжЕМДПЩЃЛЃЈ2ЃЉАб![]() ДњШыЕНЕквЛЮЪЕФgЃЈaЃЉЕФЕкЖўКЭЕкШ§ИіНтЮіЪНжаЃЌЧѓГіaЕФжЕЃЌДњШыfЃЈxЃЉжаЕУЕНfЃЈxЃЉЕФНтЮіЪНЃЌРћгУХфЗНПЩЕУfЃЈxЃЉЕФзюДѓжЕЃЎ
ДњШыЕНЕквЛЮЪЕФgЃЈaЃЉЕФЕкЖўКЭЕкШ§ИіНтЮіЪНжаЃЌЧѓГіaЕФжЕЃЌДњШыfЃЈxЃЉжаЕУЕНfЃЈxЃЉЕФНтЮіЪНЃЌРћгУХфЗНПЩЕУfЃЈxЃЉЕФзюДѓжЕЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉгЩ![]()
![]() .етРя
.етРя![]()
ЂйШє![]() дђЕБ
дђЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
ЂкШє![]() ЕБ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
ЂлШє![]() дђЕБ
дђЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
вђДЫ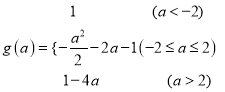
ЃЈ2ЃЉ![]()
![]() ЂйШє
ЂйШє![]() ЃЌдђга
ЃЌдђга![]() ЕУ
ЕУ![]() ЃЌУЌЖмЃЛ
ЃЌУЌЖмЃЛ
ЂкШє![]() ЃЌдђга
ЃЌдђга![]() МД
МД![]() Лђ
Лђ![]() ЃЈЩсЃЉ.
ЃЈЩсЃЉ.
![]()
![]() ЪБЃЌ
ЪБЃЌ ![]() ДЫЪБ
ДЫЪБ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ШЁЕУзюДѓжЕЮЊ5.
ШЁЕУзюДѓжЕЮЊ5.
ЕуОІЃКЖўДЮКЏЪ§дкБеЧјМфЩЯБигазюДѓжЕКЭзюаЁжЕЃЌЫќжЛФмдкЧјМфЕФЖЫЕуЛђЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуДІШЁЕНЃЛГЃМћЬтаЭгаЃКЃЈ1ЃЉжсЙЬЖЈЧјМфвВЙЬЖЈЃЛЃЈ2ЃЉжсЖЏЃЈжсКЌВЮЪ§ЃЉЃЌЧјМфЙЬЖЈЃЛЃЈ3ЃЉжсЙЬЖЈЃЌЧјМфЖЏЃЈЧјМфКЌВЮЪ§ЃЉ. евзюжЕЕФЙиМќЪЧЃКЃЈ1ЃЉЭМЯѓЕФПЊПкЗНЯђЃЛЃЈ2ЃЉЖдГЦжсгыЧјМфЕФЮЛжУЙиЯЕЃЛЃЈ3ЃЉНсКЯЭМЯѓМАЕЅЕїадШЗЖЈКЏЪ§зюжЕ.
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
21
ЁОЬтФПЁПвбжЊСНИіВЛЙВЯпЕФЯђСП![]() ЕФМаНЧЮЊ
ЕФМаНЧЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЮЊе§ЪЕЪ§.
ЮЊе§ЪЕЪ§.
ЃЈ1ЃЉШє![]() гы
гы![]() ДЙжБЃЌЧѓ
ДЙжБЃЌЧѓ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕМАЖдгІЕФ
ЕФзюаЁжЕМАЖдгІЕФ![]() ЕФжЕЃЌВЂжИГіДЫЪБЯђСП
ЕФжЕЃЌВЂжИГіДЫЪБЯђСП![]() гы
гы![]() ЕФЮЛжУЙиЯЕ.
ЕФЮЛжУЙиЯЕ.
ЃЈ3ЃЉШє![]() ЮЊШёНЧЃЌЖдгке§ЪЕЪ§
ЮЊШёНЧЃЌЖдгке§ЪЕЪ§![]() ЃЌЙигк
ЃЌЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЭЌЕФе§ЪЕЪ§НтЃЌЧв
гаСНИіВЛЭЌЕФе§ЪЕЪ§НтЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁП(1) ![]() ЃЛ(2)Д№АИМћНтЮіЃЛ(3)
ЃЛ(2)Д№АИМћНтЮіЃЛ(3) ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУ![]() +2
+2![]() гы
гы![]() Љ4
Љ4![]() ДЙжБЃЌЃЈ
ДЙжБЃЌЃЈ ![]() +2
+2![]() ЃЉЃЈ
ЃЉЃЈ![]() Љ4
Љ4![]() ЃЉ=0ЃЌПЩЕУЃЌЛЏМђЃЌМДПЩЧѓГіtanІШЃЛ
ЃЉ=0ЃЌПЩЕУЃЌЛЏМђЃЌМДПЩЧѓГіtanІШЃЛ
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§ЕФаджЪЃЌПЩЧѓ|x![]() Љ
Љ![]() |ЕФзюаЁжЕМАЖдгІЕФxЕФжЕЃЌРћгУЪ§СПЛ§ЙЋЪНЃЌПЩШЗЖЈЯђСП
|ЕФзюаЁжЕМАЖдгІЕФxЕФжЕЃЌРћгУЪ§СПЛ§ЙЋЪНЃЌПЩШЗЖЈЯђСП![]() гыx
гыx![]() Љ
Љ![]() ЕФЮЛжУЙиЯЕЃЛ
ЕФЮЛжУЙиЯЕЃЛ
ЃЈ3ЃЉЗНГЬ|x![]() Љ
Љ![]() |=|m
|=|m![]() |ЃЌЕШМлгк9x2Љ3cosІШx+1Љ9m2=0ЃЌРћгУЙигкxЕФЗНГЬ|x
|ЃЌЕШМлгк9x2Љ3cosІШx+1Љ9m2=0ЃЌРћгУЙигкxЕФЗНГЬ|x![]() Љ
Љ![]() |=|m
|=|m![]() |гаСНИіВЛЭЌЕФе§ЪЕЪ§НтЃЌНЈСЂВЛЕШЪНЃЌМДПЩШЗЖЈНсТлЃЎ
|гаСНИіВЛЭЌЕФе§ЪЕЪ§НтЃЌНЈСЂВЛЕШЪНЃЌМДПЩШЗЖЈНсТлЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉгЩЬтвтЃЌЕУ![]() МД
МД![]()
![]() ЙЪ
ЙЪ![]() гж
гж![]() ЃЌЙЪ
ЃЌЙЪ![]()
вђДЫЃЌ 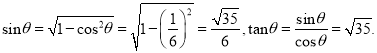
ЃЈ2ЃЉ![]()
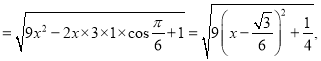 ЙЪЕБ
ЙЪЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ШЁЕУзюаЁжЕЮЊ
ШЁЕУзюаЁжЕЮЊ![]() ДЫЪБЃЌ
ДЫЪБЃЌ ![]()
ЙЪЯђСП![]() гы
гы![]() ДЙжБ.
ДЙжБ.
ЃЈ3ЃЉЖдЗНГЬ![]() СНБпЦНЗНЃЌЕУ
СНБпЦНЗНЃЌЕУ![]() Ђй
Ђй
ЩшЗНГЬЂйЕФСНИіВЛЭЌе§ЪЕЪ§НтЮЊ![]() ЃЌдђгЩЬтвтЃЌЕУ
ЃЌдђгЩЬтвтЃЌЕУ
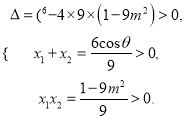 ЃЌ
ЃЌ
НтжЎЃЌЕУ![]()
Шє![]() дђЗНГЬЂйПЩвдЛЏЮЊ
дђЗНГЬЂйПЩвдЛЏЮЊ![]() ЃЌ
ЃЌ
дђ![]() МД
МД![]() гЩЬтжЊ
гЩЬтжЊ![]() ЙЪ
ЙЪ![]()
Сю![]() ЃЌЕУ
ЃЌЕУ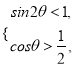 ЃЌЙЪ
ЃЌЙЪ![]() ЃЌЧв
ЃЌЧв![]() .
.
ЕБ![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌ
ЪБЃЌ ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЌЧв
ЃЌЧв![]() }ЃЛ
}ЃЛ
ЕБ![]() ЃЌЛђ
ЃЌЛђ![]() ЪБЃЌ
ЪБЃЌ ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌBC=aЃЌAC=bЃЌЧвaЃЌbЪЧЗНГЬ![]() ЕФСНИљЃЌ2cos(A+B)=1ЃЎ
ЕФСНИљЃЌ2cos(A+B)=1ЃЎ
(1)ЧѓЁЯCЕФЖШЪ§ЃЛ
(2)ЧѓABЕФГЄЃЛ
(3)ЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§Ш§РтжљABCЉA1B1C1жаЃЌЕуDЪЧBCЕФжаЕуЃЎ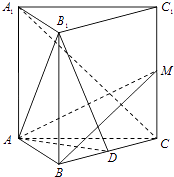
ЃЈ1ЃЉЧѓжЄЃКA1CЁЮЦНУцAB1DЃЛ
ЃЈ2ЃЉЩшMЮЊРтCC1ЕФЕуЃЌЧвТњзуBMЁЭB1DЃЌЧѓжЄЃКЦНУцAB1DЁЭЦНУцABMЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЭждВEЃК ![]() ЃЈaЃОbЃО0ЃЉЙ§ЕуЃЈ
ЃЈaЃОbЃО0ЃЉЙ§ЕуЃЈ ![]() ЃЌ1ЃЉЃЌЧвгыжБЯп
ЃЌ1ЃЉЃЌЧвгыжБЯп ![]() x+2yЉ4=0ЯрЧаЃЎ
x+2yЉ4=0ЯрЧаЃЎ
ЃЈ1ЃЉЧѓЭждВEЕФЗНГЬЃЛ
ЃЈ2ЃЉШєЭждВEгыxжсНЛгкMЁЂNСНЕуЃЌЭждВEФкВПЕФЖЏЕуPЪЙ|PM|ЁЂ|PO|ЁЂ|PN|ГЩЕШБШЪ§СаЃЌЧѓ ![]()
![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ ![]() ADгыBCНЛгкЕуMЃЌЩш
ADгыBCНЛгкЕуMЃЌЩш![]() ЃЌвд
ЃЌвд![]() ЁЂ
ЁЂ![]() ЮЊЛљЕзБэЪО
ЮЊЛљЕзБэЪО![]()

ЁОД№АИЁП![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКгЩAЁЂMЁЂDШ§ЕуЙВЯпЃЌжЊ![]() ЃЛгЩCЁЂMЁЂBШ§ЕуЙВЯпЃЌжЊ
ЃЛгЩCЁЂMЁЂBШ§ЕуЙВЯпЃЌжЊ![]()
ЃЌЫљвд ЃЌЫљвд
ЃЌЫљвд![]() =
=![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃК
Щш![]() ЃЌ
ЃЌ
дђ![]()
вђЮЊAЁЂMЁЂDШ§ЕуЙВЯпЃЌЫљвд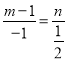 ЃЌМД
ЃЌМД![]()
гж![]()
вђЮЊCЁЂMЁЂBШ§ЕуЙВЯпЃЌЫљвд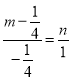 ЃЌМД
ЃЌМД![]()
гЩ![]() НтЕУ
НтЕУ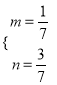 ЃЌЫљвд
ЃЌЫљвд![]()
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
20
ЁОЬтФПЁПКЏЪ§![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() МАДЫЪБ
МАДЫЪБ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђ
ЃЈ1ЃЉ![]()
ЃЈ2ЃЉ![]()
ЁОД№АИЁП(1) ![]() ЃЛ(2)
ЃЛ(2) ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧаЛЏЯвПЩЕУШ§НЧКЏЪ§ЪНЕФжЕЮЊЃ1
ЃЈ2ЃЉНсКЯШ§НЧКЏЪ§ЕФаджЪПЩЕУШ§НЧКЏЪ§ЪНЕФжЕЮЊ![]()
ЪдЬтНтЮіЃК
ЃЈ1ЃЉtan70Ёуcos10ЁуЃЈ ![]() tan20ЁуЉ1ЃЉ
tan20ЁуЉ1ЃЉ
=cot20Ёуcos10ЁуЃЈ ![]() Љ1ЃЉ
Љ1ЃЉ
=cot20Ёуcos10ЁуЃЈ![]() ЃЉ
ЃЉ
=![]() ЁСcos10ЁуЁСЃЈ
ЁСcos10ЁуЁСЃЈ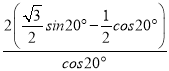 ЃЉ
ЃЉ
=![]() ЁСcos10ЁуЁСЃЈ
ЁСcos10ЁуЁСЃЈ![]() ЃЉ
ЃЉ
=![]() ЁСЃЈЉ
ЁСЃЈЉ![]() ЃЉ
ЃЉ
=Љ1
ЃЈ2ЃЉЁпЃЈ1+tan1ЁуЃЉЃЈ1+tan44ЁуЃЉ=1+ЃЈtan1Ёу+tan44ЁуЃЉ+tan1Ёуtan44Ёу
=1+tanЃЈ1Ёу+44ЁуЃЉ[1Љtan1Ёуtan44Ёу]+tan1Ёуtan44Ёу=2ЃЎ
ЭЌРэПЩЕУЃЈ1+tan2ЁуЃЉЃЈ1+tan43ЁуЃЉ
=ЃЈ1+tan3ЁуЃЉЃЈ1+tan42ЁуЃЉ
=ЃЈ1+tan4ЁуЃЉЃЈ1+tan41ЁуЃЉ=Ё=2ЃЌ
ЙЪ![]() =
=![]()
ЕуОІЃКШ§НЧКЏЪ§ЪНЕФЛЏМђвЊзёбЁАШ§ПДЁБддђ:вЛПДНЧЃЌетЪЧживЊвЛЛЗЃЌЭЈЙ§ПДНЧжЎМфЕФВюБ№гыСЊЯЕЃЌАбНЧНјааКЯРэЕФВ№ЗжЃЌДгЖје§ШЗЪЙгУЙЋЪН ЃЛЖўПДКЏЪ§УћГЦЃЌПДКЏЪ§УћГЦжЎМфЕФВювьЃЌДгЖјШЗЖЈЪЙгУЕФЙЋЪНЃЌГЃМћЕФгаЧаЛЏЯвЃЛШ§ПДНсЙЙЬиеїЃЌЗжЮіНсЙЙЬиеїЃЌПЩвдАяжњЮвУЧевЕНБфаЮЕФЗНЯђЃЌШчгіЕНЗжЪНвЊЭЈЗжЕШ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
18
ЁОЬтФПЁПЦНУцФкИјЖЈШ§ИіЯђСП![]()
ЃЈ1ЃЉЧѓ![]()
ЃЈ2ЃЉЧѓТњзу![]() ЕФЪЕЪ§
ЕФЪЕЪ§![]() .
.
ЃЈ3ЃЉШє![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ТњзуЃК2a1+22a2+23a3+Ё+2nan=nЃЈnЁЪN*ЃЉЃЌЪ§Са{ ![]() }ЕФЧАnЯюКЭЮЊSn ЃЌ дђS1S2S3ЁS10= ЃЎ
}ЕФЧАnЯюКЭЮЊSn ЃЌ дђS1S2S3ЁS10= ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧЮвЙњЙХДњЪ§бЇОЕфУћжјЃЌЫќдкМЏКЯбЇжаЕФбаОПБШЮїЗНдч1ЧЇФъЃЌдкЁЖОХеТЫуЪѕЁЗжаЃЌНЋЫФИіУцОљЮЊжБНЧШ§НЧаЮЕФЫФУцЬхГЦЮЊБюФЃЌвбжЊФГЁАБюФЁБЕФШ§ЪгЭМШчЭМЫљЪОЃЌдђИУБюФЕФЭтНгЧђЕФБэУцЛ§ЮЊЃЈ ЃЉ 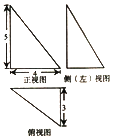
A.200Іа
B.50Іа
C.100Іа
D.![]() Іа
Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЈвхдкRЩЯЕФКЏЪ§fЃЈxЃЉ=ex+mx2ЉmЃЈmЃО0ЃЉЃЌЕБx1+x2=1ЪБЃЌВЛЕШЪНfЃЈx1ЃЉ+fЃЈ0ЃЉЃОfЃЈx2ЃЉ+fЃЈ1ЃЉКуГЩСЂЃЌдђЪЕЪ§x1ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈЉЁоЃЌ0ЃЉ
B.![]()
C.![]()
D.ЃЈ1ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com