
【题目】《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( ) 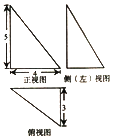
A.200π
B.50π
C.100π
D.![]() π
π
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且与直线
,1),且与直线 ![]() x+2y﹣4=0相切.
x+2y﹣4=0相切.
(1)求椭圆E的方程;
(2)若椭圆E与x轴交于M、N两点,椭圆E内部的动点P使|PM|、|PO|、|PN|成等比数列,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 及此时
及此时![]() 的最大值.
的最大值.
【答案】(1) 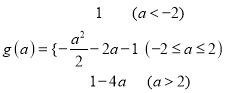 ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)利用同角三角函数间的基本关系化简函数解析式后,分三种情况:①![]() 小于﹣1时②
小于﹣1时②![]() 大于﹣1而小于1时③
大于﹣1而小于1时③![]() 大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把
大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把![]() 代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
试题解析:
(1)由![]()
![]() .这里
.这里![]()
①若![]() 则当
则当![]() 时,
时, ![]()
②若![]() 当
当![]() 时,
时, ![]()
③若![]() 则当
则当![]() 时,
时, ![]()
因此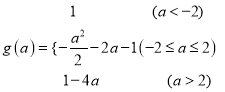
(2)![]()
![]() ①若
①若![]() ,则有
,则有![]() 得
得![]() ,矛盾;
,矛盾;
②若![]() ,则有
,则有![]() 即
即![]() 或
或![]() (舍).
(舍).
![]()
![]() 时,
时, ![]() 此时
此时![]()
当![]() 时,
时, ![]() 取得最大值为5.
取得最大值为5.
点睛:二次函数在闭区间上必有最大值和最小值,它只能在区间的端点或二次函数图象的顶点处取到;常见题型有:(1)轴固定区间也固定;(2)轴动(轴含参数),区间固定;(3)轴固定,区间动(区间含参数). 找最值的关键是:(1)图象的开口方向;(2)对称轴与区间的位置关系;(3)结合图象及单调性确定函数最值.
【题型】填空题
【结束】
21
【题目】已知两个不共线的向量![]() 的夹角为
的夹角为![]() ,且
,且![]() 为正实数.
为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() ;
;
(2)若![]() ,求
,求![]() 的最小值及对应的
的最小值及对应的![]() 的值,并指出此时向量
的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数
为锐角,对于正实数![]() ,关于
,关于![]() 的方程
的方程![]() 有两个不同的正实数解,且
有两个不同的正实数解,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com