
【题目】在三棱柱![]() 中,侧面
中,侧面![]() 为菱形,且
为菱形,且![]() ,点E,F分别为
,点E,F分别为![]() ,
,![]() 的中点.求证:
的中点.求证:
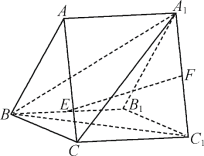
(1)平面![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x﹣2)![]() ax2+ax(a∈R).
ax2+ax(a∈R).
(1)当a=1时,求f(x)的极值;
(2)若f(x)恰有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2+pn,且a4,a7,a12成等比数列.
(1)求数列{an}的通项公式;
(2)若bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(3)判断数列![]() 中是否存在三项成等差数列,并证明你的结论.
中是否存在三项成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
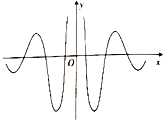
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办的体育节设有投篮项目.该项目规定:每位同学仅有三次投篮机会,其中前两次投篮每投中一次得1分,第三次投篮投中得2分,若不中不得分,投完三次后累计总分.
(1)若甲同学每次投篮命中的概率为![]() ,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
,且相互不影响,记甲同学投完三次后的总分为X,求随机变量X的概率分布列;
(2)若(1)中的甲同学邀请乙同学一起参加投篮项目,已知乙同学每次投篮命中的概率为![]() ,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
,且相互不影响,甲、乙两人之间互不干扰.求甲同学的总分低于乙同学的总分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运用祖暅原理计算球的体积时,夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意一个平面所截,若截面面积都相等,则这两个几何体的体积相等.构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆![]() 绕y轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
绕y轴旋转一周后得一橄榄状的几何体(如图③),类比上述方法,运用祖暅原理可求得其体积等于( )
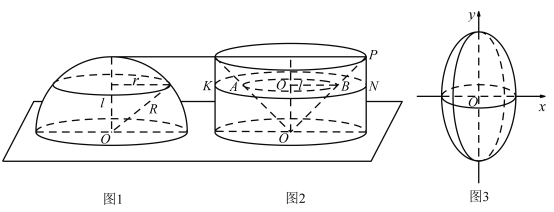
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
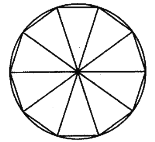
【题目】在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正![]() 边形等分成
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(
变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(![]() 取近似值3.14)
取近似值3.14)
A.0.012B.0.052
C.0.125D.0.235
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com