
【题目】已知动圆![]() 过定点
过定点![]() 且与
且与![]() 轴相切,点
轴相切,点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)一条直线经过点![]() ,且交曲线
,且交曲线![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 为直线
为直线![]() 上的动点.
上的动点.
①求证:![]() 不可能是钝角;
不可能是钝角;
②是否存在这样的点![]() ,使得
,使得![]() 是正三角形?若存在,求点
是正三角形?若存在,求点![]() 的坐标:否则,说明理由.
的坐标:否则,说明理由.
科目:高中数学 来源: 题型:
【题目】下列命题中不正确的个数是( )
①若直线![]() 上有无数个点不在平面
上有无数个点不在平面![]() 内,则
内,则![]() ;
;
②和两条异面直线都相交的两条直线异面;
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;
④一条直线和两条异面直线都相交,则它们可以确定两个平面.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() 点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,
点D,E分别为棱PA,PC的中点,M是线段AD的中点,N是线段BC的中点,![]() ,
,![]() .
.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BDE;
平面BDE;
![]() Ⅱ
Ⅱ![]() 求直线MN到平面BDE的距离;
求直线MN到平面BDE的距离;
![]() Ⅲ
Ⅲ![]() 求二面角
求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆C:
是椭圆C:![]() 上的一点,椭圆C的离心率与双曲线
上的一点,椭圆C的离心率与双曲线![]() 的离心率互为倒数,斜率为
的离心率互为倒数,斜率为![]() 直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
直线l交椭圆C于B,D两点,且A、B、D三点互不重合.
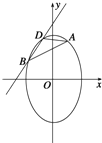
(1)求椭圆C的方程;
(2)若![]() 分别为直线AB,AD的斜率,求证:
分别为直线AB,AD的斜率,求证:![]() 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com