
【题目】函数![]() ,
,
(1)设函数![]() 的定义域为A
的定义域为A
①若![]() ,
,![]() ,
,![]() ,求实数c的值.
,求实数c的值.
②若![]() ,
,![]() ,
,![]() ,求M的最小值
,求M的最小值
(2)若![]() ,对任意的
,对任意的![]() ,存在
,存在![]() ,使得不等式
,使得不等式![]() 成立,求实数n的取值范围.
成立,求实数n的取值范围.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)①依题意可知![]() 的解集为
的解集为![]() ,则
,则![]() 与
与![]() 为方程
为方程![]() 的两根,利用韦达定理得到方程组解得即可;
的两根,利用韦达定理得到方程组解得即可;
②依题意可知![]() 恒成立,即
恒成立,即![]() 即可得到
即可得到![]() ,所以
,所以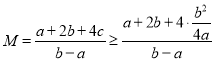 在利用基本不等式计算可得;
在利用基本不等式计算可得;
(2)依题意可知对任意的![]() ,存在
,存在![]() ,使得不等式
,使得不等式![]() 成立,根据二次函数的性质计算
成立,根据二次函数的性质计算![]() 的最小值,从而得出
的最小值,从而得出![]() 与
与![]() 之间的关系,分离参数得出
之间的关系,分离参数得出![]() ,求出右侧函数的最大值即可得出
,求出右侧函数的最大值即可得出![]() 的范围.
的范围.
解:(1)①当![]() ,
,![]() ,
,![]() ,即
,即![]() 的解集为
的解集为![]() ,
,
则![]() 与
与![]() 为方程
为方程![]() 的两根,
的两根,
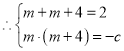 解得
解得![]()
②若![]() ,
,![]() ,即
,即![]() 恒成立,
恒成立,
![]() 即
即![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]()
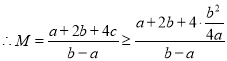
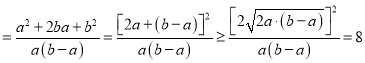
当且仅当![]() 时取等号,
时取等号,
所以![]() 的最小值为
的最小值为![]()
(2)若![]() ,对任意的
,对任意的![]() ,存在
,存在![]() ,使得不等式
,使得不等式![]() 成立
成立
即对任意的![]() ,存在
,存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
即![]() ,
,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]()
所以![]()
因为![]() ,
,
所以![]()
因为![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,![]()
所以![]()
即![]()


科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,试求抽取3人中恰有2人是“微信控”的概率.
参考公式: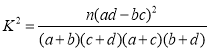 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.040 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=![]() ,点E是棱PB的中点.
,点E是棱PB的中点.

(1)求异面直线EC与PD所成角的余弦值;
(2)求二面角B-EC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,圆
,圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() ,试判断
,试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元).每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部销售完.
(万元).每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)如图所示,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .将四边形
.将四边形![]() 沿对角线
沿对角线![]() 折成四面体
折成四面体![]() ,使平面
,使平面![]() 平面
平面![]() ,则下列结论错误的结论是( )
,则下列结论错误的结论是( )
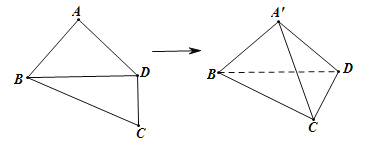
A.![]() B.
B.![]()
C.![]() 与平面
与平面![]() 所成的角为30°D.四面体
所成的角为30°D.四面体![]() 的体积为
的体积为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com