
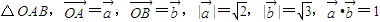 ,边AB上一点P1,这里P1异于A、B.由P1引边OB的垂线P1Q1,Q1是垂足,再由Q1引边OA的垂线Q1R1,R1是垂足.又由R1引边AB的垂线R1P2,P2是垂足.同样的操作连续进行,得到点 Pn、Qn、Rn(n∈N*).设
,边AB上一点P1,这里P1异于A、B.由P1引边OB的垂线P1Q1,Q1是垂足,再由Q1引边OA的垂线Q1R1,R1是垂足.又由R1引边AB的垂线R1P2,P2是垂足.同样的操作连续进行,得到点 Pn、Qn、Rn(n∈N*).设 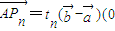 <tn<1),如图.
<tn<1),如图.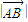 的值;
的值;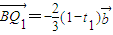 ,问该同学这个结论是否正确?并说明理由;
,问该同学这个结论是否正确?并说明理由;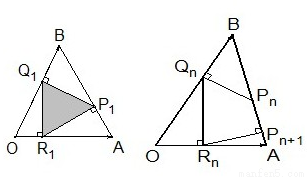
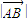 的值,先求其平方.利用三角形OAB中的边角条件即可求得
的值,先求其平方.利用三角形OAB中的边角条件即可求得 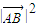 ,从而得出
,从而得出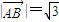 ;
;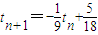 变形为:
变形为: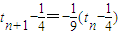 得到{tn-
得到{tn- }构成一个等比数列,公比为-
}构成一个等比数列,公比为- ,利用等比数列的通项公式即可表示出tn
,利用等比数列的通项公式即可表示出tn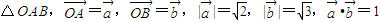 -----(1分)
-----(1分) ;所以,
;所以,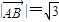 --------------(4分)
--------------(4分)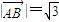 ,
,
 -----------------(6分)
-----------------(6分)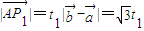 ,则
,则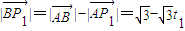
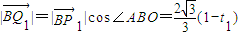 ,所以,
,所以,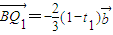 ---------(8分)
---------(8分)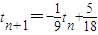 ---------------------(14分)
---------------------(14分) ------------------------(16分)
------------------------(16分) }构成一个等比数列,公比为-
}构成一个等比数列,公比为- ,
,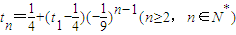 --------------(18分)
--------------(18分)

 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
| OP |
| PB |
| OQ |
| AP |
| RO |
| RA |
| RB |
查看答案和解析>>
科目:高中数学 来源:0103 期末题 题型:解答题
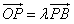 ,点Q是边AB上一点,且
,点Q是边AB上一点,且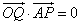 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| OP |
| PB |
| OQ |
| AP |
| RO |
| RA |
| RB |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏州市常熟市高一(上)期末数学模拟试卷(解析版) 题型:解答题
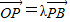 ,点Q是边AB上一点,且
,点Q是边AB上一点,且 .
.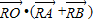 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com