Question

【题目】已知，

（1）若展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大项

的系数；

（2）若展开式前三项的二项式系数和等于79，求展开式中系数最大的项．

Answer 1

【答案】（1）70（2）（2x）10

【解析】

试题分析：（1）第k+1项的二项式系数为，由题意可得关于n的方程，求出n．而二项式系数最大的项为中间项，n为奇数时，中间两项二项式系数相等；n为偶数时，中间只有一项．（2）由展开式前三项的二项式系数和等于79，可得关于n的方程，求出n．而求展开式中系数最大的项时，可通过解不等式组求得，假设项的系数最大，项的系数为，则有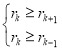

试题解析：（1）通项Tr＋1＝n－r·（2x）r＝22r－nxr，（此题可以用组合数表示结果）

由题意知，，成等差数列，

∴＝，∴n＝14或7.

当n＝14时，第8项的二项式系数最大，该项的系数为22×7－14＝3 432；

当n＝7时，第4、5项的二项式系数相等且最大，

其系数分别为22×3－7=，22×4－7=70.

（2）由题意知＝79，

∴n＝12或n＝－13（舍）．

∴Tr＋1＝22r－12xr.

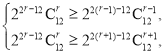由得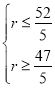 ∴r＝10.

∴展开式中系数最大的项为T11＝22×10－12·x10＝（2x）10.