
【题目】在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将梯形
的中点,将梯形![]() 绕
绕![]() 旋转
旋转![]() ,得到梯形
,得到梯形![]() (如图).
(如图).
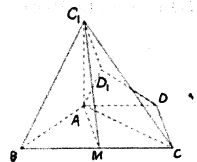
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出BC∥平面ADD',BC'∥平面ADD',从而平面BCC'∥平面ADD',由此能证明NC'∥平面ADD'.
(2)以A为原点,AB为x轴,AC为y轴,AC′为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣C'N﹣C的余弦值.
(1)证明:∵BC∥AD,∴BC∥平面ADD',
同理BC'∥平面ADD',
又BC∩BC'=B,∴平面BCC'∥平面ADD',
∵NC'平面BCC',∴NC'∥平面ADD'.
(2)解:![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,又
,又![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,又
,又
![]() ,
,![]() ,
,![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]()
![]() ,即
,即![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
如图建立空间直角坐标系,
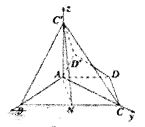
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() .
.
则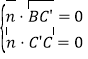 即
即![]()
取![]() ,则
,则![]() ,
,![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,又
,又![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 则为
则为![]() 的中点,
的中点,![]() ,
,![]() 平面
平面![]() 的法向量
的法向量
![]() .
.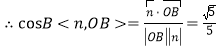 ,
,
由图形可知二面角![]() 为钝角,所以二面角
为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,
(1)若展开式中第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大项
的系数;
(2)若展开式前三项的二项式系数和等于79,求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有5个男生和3个女生,从中选出5人担任5门不同学科的科代表,求分别符合下列条件的选法数.
(1)某女生一定担任语文科代表;
(2)某男生必须包括在内,但不担任语文科代表;
(3)某女生一定要担任语文科代表,某男生必须担任科代表,但不担任数学科代表.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏厂商对新出品的一款游戏设定了“防沉迷系统”,规则如下:
①3小时以内(含3小时)为健康时间,玩家在这段时间内获得的累积经验值![]() 单位:
单位:![]() 与游玩时间
与游玩时间![]() 小时)满足关系式:
小时)满足关系式:![]() ;
;
②3到5小时(含5小时)为疲劳时间,玩家在这段时间内获得的经验值为![]() 即累积经验值不变);
即累积经验值不变);
③超过5小时为不健康时间,累积经验值开始损失,损失的经验值与不健康时间成正比例关系,比例系数为50.
⑴当![]() 时,写出累积经验值E与游玩时间t的函数关系式
时,写出累积经验值E与游玩时间t的函数关系式![]() ,并求出游玩6小时的累积经验值;
,并求出游玩6小时的累积经验值;
⑵该游戏厂商把累积经验值E与游玩时间t的比值称为“玩家愉悦指数”,记作![]() ;若
;若![]() ,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某服装厂每天的固定成本是30000元,每天最大规模的生产量是![]() 件.每生产一件服装,成本增加100元,生产
件.每生产一件服装,成本增加100元,生产![]() 件服装的收入函数是
件服装的收入函数是![]() ,记
,记![]() ,
,![]() 分别为每天生产
分别为每天生产![]() 件服装的利润和平均利润(
件服装的利润和平均利润(![]() ).
).
(1)当![]() 时,每天生产量
时,每天生产量![]() 为多少时,利润
为多少时,利润![]() 有最大值;
有最大值;
(2)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 有最大值,并求
有最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】物联网兴起、发展、完善极大的方便了市民生活需求.某市统计局随机地调查了该市某社区的100名市民网上购菜状况,其数据如下:
每周网上买菜次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 | 总计 |
男 | 10 | 8 | 7 | 3 | 2 | 15 | 45 |
女 | 5 | 4 | 6 | 4 | 6 | 30 | 55 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 | 100 |
(1)把每周网上买菜次数超过3次的用户称为“网上买菜热爱者”,能否在犯错误概率不超过0.005的前提下,认为是否为“网上买菜热爱者”与性别有关?
(2)把每周使用移动支付6次及6次以上的用户称为“网上买菜达人”,视频率为概率,在我市所有“网上买菜达人”中,随机抽取4名用户求既有男“网上买菜达人”又有女“网上买菜达人”的概率.
附公式及表如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
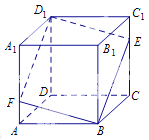
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三边长分别为a、b、c,且满足![]() .
.
(1)是否存在边长均为整数的△ABC?若存在,求出三边长;若不存在,说明理由.
(2)若![]() ,
,![]() ,
,![]() ,求出△ABC周长的最小值.
,求出△ABC周长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ω>0,0<φ<π,直线![]() 和
和![]() 是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的
是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的![]() 倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
A.![]() B.
B.![]()
C.y=2cos2xD.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com