
【题目】在三棱锥P﹣ABC中,D为AB的中点.
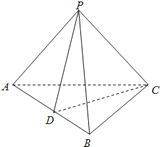
(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
【答案】(1)![]() 为
为![]() 中点(2)详见解析
中点(2)详见解析
【解析】试题分析:(1)根据线面平行的性质进行判断即可:
(2)根据面面垂直的性质定理进行证明.
(1)解:E为AC中点.理由如下:
平面PDE交AC于E,
即平面PDE∩平面ABC=DE,
而BC∥平面PDF,BC平面ABC,
所以BC∥DE,
在△ABC中,因为D为AB的中点,所以E为AC中点;
(2)证:因为PA=PB,D为AB的中点,
所以AB⊥PD,
因为平面PCD⊥平面ABC,平面PCD∩平面ABC=CD,
在锐角△PCD所在平面内作PO⊥CD于O,
则PO⊥平面ABC,
因为AB平面ABC,
所以PO⊥AB
又PO∩PD=P,PO,PD平面PCD,
则AB⊥平面PCD,
又PC平面PCD,
所以AB⊥PC.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其导函数设为
,其导函数设为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,若![]() 的极值点恰为
的极值点恰为![]() 的零点,试求
的零点,试求![]() ,
,![]() 这两个函数的所有极值之和的取值范围.
这两个函数的所有极值之和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (m,n为常数),在
(m,n为常数),在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的解析式并写出定义域;
的解析式并写出定义域;
(Ⅱ)若![]() ,使得对
,使得对![]() 上恒有
上恒有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() 有两个不同的零点
有两个不同的零点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 折起,则下列说法正确的是______________.
折起,则下列说法正确的是______________.
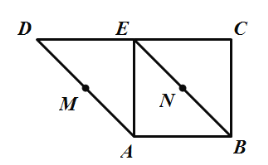
(1)不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内),都有
内),都有![]() 平面
平面![]() ;
;
(2)不论![]() 折至何位置,都有
折至何位置,都有![]() ;
;
(3)不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内),都有
内),都有![]() ;
;
(4)在折起过程中,一定存在某个位置,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 满足,存在实数
满足,存在实数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 有上界,
有上界,![]() 是数列
是数列![]() 的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
的一个上界,已知定理:单调递增有上界的数列收敛(即极限存在).
(1)数列![]() 是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
是否存在上界?若存在,试求其所有上界中的最小值;若不存在,请说明理由;
(2)若非负数列![]() 满足
满足![]() ,
,![]() (
(![]() ),求证:1是非负数列
),求证:1是非负数列![]() 的一个上界,且数列
的一个上界,且数列![]() 的极限存在,并求其极限;
的极限存在,并求其极限;
(3)若正项递增数列![]() 无上界,证明:存在
无上界,证明:存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1是某条公共汽车线路收支差额![]() 与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象判断下列说法正确的是( )
与乘客量的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为盈的建议,如图2、3所示.你能根据图象判断下列说法正确的是( )
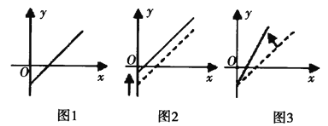
①图2的建议为减少运营成本;②图2的建议可能是提高票价;
③图3的建议为减少运营成本;④图3的建议可能是提高票价.
A.①④B.②④C.①③D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com