
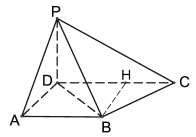
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
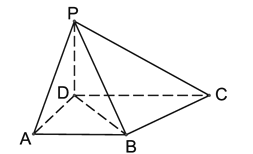
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为棱
为棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)过![]() 作
作![]() 于
于![]() ,根据条件可证明
,根据条件可证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再由面面垂直的的判定即可得证;(2)根据条件可作出二面角
,再由面面垂直的的判定即可得证;(2)根据条件可作出二面角![]() 的平面角,从而即可建立关于
的平面角,从而即可建立关于![]() 的方程,或建立空间直角坐标系,求得两个平面的法向量后亦可建立关于
的方程,或建立空间直角坐标系,求得两个平面的法向量后亦可建立关于![]() 的方程,从而求解.
的方程,从而求解.
试题解析:(1)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,在梯形
,在梯形![]() 中,过点作
中,过点作![]() 作
作![]() 于
于![]() ,
,
在![]() 中,
中,![]() ,又在
,又在![]() 中,
中,![]() ,
,
∴![]() , ∵
, ∵![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() ,∵
,∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;(2)法一:过点
;(2)法一:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连
,连![]() ,由(1)可知
,由(1)可知![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,由(1)知
,由(1)知![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴![]()
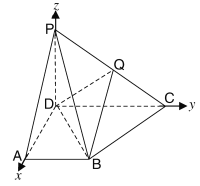
![]() ;法二:以
;法二:以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系(如图)
轴建立空间直角坐标系(如图)
则![]() ,
,![]() ,
,![]() ,
,![]() ,令
,令![]() ,则
,则
![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则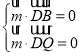 ,即
,即 ![]() 即
即 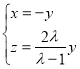 ,
,
不妨令![]() ,得
,得![]() ,∵二面角
,∵二面角![]() 为
为![]() ,
,
∴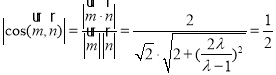 ,解得
,解得![]() , ∵
, ∵![]() 在棱
在棱![]() 上,∴
上,∴![]() ,故
,故![]() 为所求.
为所求.



 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】某企业节能降耗技术改造后,在生产某产品过程中几录的产量x(吨)与相应的生产能耗y(吨)的几 组对应数据如表所示:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | a |
若根据表中数据得出y关于x的线性回归方程为 ![]() =0.7x+0.35,则表中a的值为( )
=0.7x+0.35,则表中a的值为( )
A.3
B.3.15
C.3.5
D.4.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2),B(4,6), ![]() =t1
=t1 ![]() +t2
+t2 ![]() ,其中t1、t2为实数;
,其中t1、t2为实数;
(1)若点M在第二或第三象限,且t1=2,求t2的取值范围;
(2)求证:当t1=1时,不论t2为何值,A、B、M三点共线;
(3)若t1=a2 , ![]() ⊥
⊥ ![]() ,且△ABM的面积为12,求a和t2的值.
,且△ABM的面积为12,求a和t2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为 ![]() ),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( ) 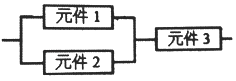
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,E是BC的中点,F是DD1的中点, 
(1)求证:CF∥平面A1DE;
(2)求二面角A1﹣DE﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数 ![]() ,x∈[0,9]的值域为集合B,
,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B)C,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com