
【题目】如图,已知平面![]() 平面
平面![]() ,
,![]() ,
,![]() .求:
.求:
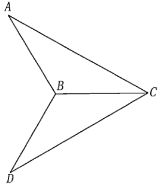
(1)![]() 与
与![]() 所成角;
所成角;
(2)![]() 与平面
与平面![]() 所成角;
所成角;
(3)二面角![]() 大小.
大小.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)作![]() 于点
于点![]() ,连接
,连接![]() ,由题意结合面面垂直的性质、平面几何知识可得
,由题意结合面面垂直的性质、平面几何知识可得![]() 、
、![]() 、
、![]() 两两垂直,建立空间直角坐标系,求出各点坐标后,利用
两两垂直,建立空间直角坐标系,求出各点坐标后,利用![]() 即可得解;
即可得解;
(2)求出![]() 的方向向量
的方向向量![]() 和平面
和平面![]() 的一个法向量为
的一个法向量为![]() ,利用
,利用![]() 求得线面角的正弦值后即可得解;
求得线面角的正弦值后即可得解;
(3)求得平面![]() 的一个法向量为
的一个法向量为![]() ,利用
,利用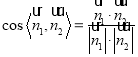 即可得解.
即可得解.
(1)作![]() 于点
于点![]() ,连接
,连接![]() ,
,
因为平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,
如图建立直角坐标系![]() ,
,
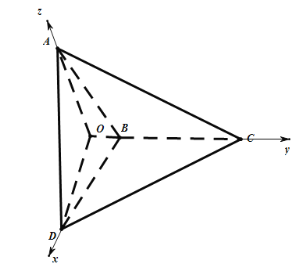
设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,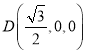 ,
,![]() ,
,![]() ,
,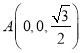 ,
,
所以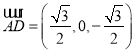 ,
,![]() ,
,
所以![]() ,
,
所以![]() 与
与![]() 所成角为
所成角为![]() ;
;
(2)由(1)知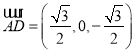 ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则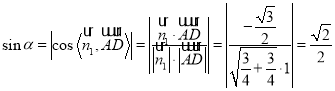 ,
,
所以![]() 即
即![]() 与平面
与平面![]() 所成角为
所成角为![]() ;
;
(3)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由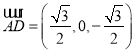 ,
,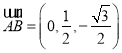 可得
可得
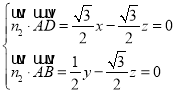 ,令
,令![]() ,则
,则![]() ,
,
所以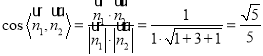 ,
,
又![]() 为钝二面角,
为钝二面角,
∴二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(1)求取出的4个球均为黑球的概率.
(2)求取出的4个球中恰有1个红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某海岸P的附近有三个岛屿Q,R,S,计划建立三座独立大桥,将这四个地方连起来,每座桥只连接两个地方,且不出现立体交叉形式,则不同的连接方式有( ).
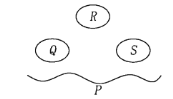
A.24种B.20种C.16种D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若有平面![]() 与
与![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则下列命题中真命题的序号有________.(1)过点
,则下列命题中真命题的序号有________.(1)过点![]() 且垂直于
且垂直于![]() 的直线平行于
的直线平行于![]() ;(2)过点
;(2)过点![]() 且垂直于
且垂直于![]() 的平面垂直于
的平面垂直于![]() ;(3)过点
;(3)过点![]() 且垂直于
且垂直于![]() 的直线在
的直线在![]() 内;(4)过点
内;(4)过点![]() 且垂直于
且垂直于![]() 的直线在
的直线在![]() 内.
内.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为 _________ .(结果用最简分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为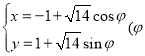 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 的交线为直线
的交线为直线![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,现沿对角线
,现沿对角线![]() 将
将![]() 折起,使点A到达点P,点M,N分别在直线
折起,使点A到达点P,点M,N分别在直线![]() ,
,![]() 上,且A,B,M,N四点共面.
上,且A,B,M,N四点共面.
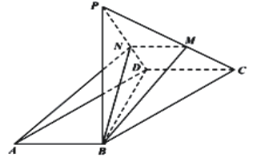
(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,二面角
,二面角![]() 平面角大小为
平面角大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com