
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
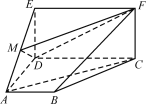
【答案】(1)详见解析;(2)1:4.
【解析】
试题(1)要使得AC∥平面DMF,需要使得AC平行平面DMF内的一条直线.为了找这条直线,需要作一个过AC而与平面DMF相交的平面.为此,连结CE,交DF于N,连结MN,这样只要AC∥MN即可.因为N为线段DF的中点,所以只需M是线段AE的中点即可.
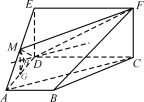
(2)一般地,求不规则的几何体的体积,可将其割为规则的几何体或补为规则的几何体.在本题中,可将几何体ADE-BCF补成三棱柱ADE-BCF,如图.这样利用柱体和锥体的体积公式即可得其体积之比.
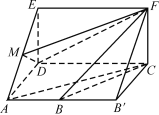
(1)当M是线段AE的中点时,AC∥平面DMF.
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN![]() 平面DMF,又AC
平面DMF,又AC![]() 平面DMF,
平面DMF,
所以AC∥平面DMF. 4分
(2)如图,将几何体ADE-BCF补成三棱柱ADE-BCF,

三棱柱ADE-BCF的体积为![]() ,
,
则几何体ADE-BCF的体积
![]() =
=![]() .
.
三棱锥F-DEM的体积V三棱锥M-DEF=![]() ,
,
故两部分的体积之比为![]() (答14,4,41均可). 12分
(答14,4,41均可). 12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 底面
底面![]() ,
,![]() 是
是![]() 上的任意一点.
上的任意一点.
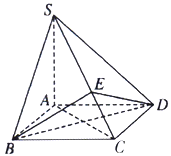
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,是否存在点
,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ?如果存在,求出点
?如果存在,求出点![]() 的位置,如果不存在,请说明理由.
的位置,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,近年看电子书的国人越来越多;所以近期有许多人呼呼“回归纸质书”,目前出版物阅读中纸质书占比出现上升现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数![]() .将这200人按年龄分成五组:第l组
.将这200人按年龄分成五组:第l组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中统计看纸质书的人得到的频率分布直方图如图所示.
,其中统计看纸质书的人得到的频率分布直方图如图所示.
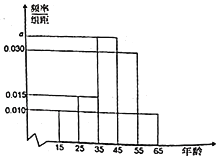
(1)求![]() 的值及看纸质书的人的平均年龄;
的值及看纸质书的人的平均年龄;
(2)按年龄划分,把年龄在![]() 的称青壮年组,年龄在
的称青壮年组,年龄在![]() 的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面
的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
看电子书 | 看纸质书 | 合计 | |
青壮年 | |||
中老年 | |||
合计 |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)若![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
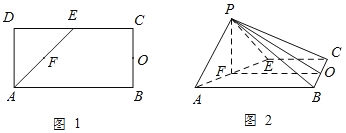
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E,F,O分别为DC,AE,BC的中点.以AE为折痕把△ADE折起,使点D到达点P的位置,且平面PAE⊥平面ABCE(如图2).
(Ⅰ)求证:BC⊥平面POF;
(Ⅱ)求直线PA与平面PBC所成角的正弦值;
(Ⅲ)在线段PE上是否存在点M,使得AM∥平面PBC?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )

A.BE∥平面PAD,且BE到平面PAD的距离为![]()
B.BE∥平面PAD,且BE到平面PAD的距离为![]()
C.BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D.BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法错误的是( )
A.若“p∨q”为假命题,则p,q均为假命题
B.“x=1”是“x≥1”的充分不必要条件
C.“sinx=![]() ”的必要不充分条件是“x=
”的必要不充分条件是“x=![]() ”
”
D.若命题p:x0∈R,x02≥0,则命题¬p:x∈R,x2<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com