
【题目】如图,四面体ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中点,E是BD的中点.
,O是AC的中点,E是BD的中点.
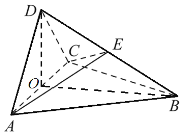
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)根据等腰三角形的性质得到![]() ,在根据面面垂直的性质定理,证得
,在根据面面垂直的性质定理,证得![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点建立空间直角坐标系,利用平面
为坐标原点建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值.
的余弦值.
(1)证明:∵ AD=CD=![]() ,O是AC的中点,
,O是AC的中点,
∴ DO⊥AC.
∵ 平面DAC⊥底面ABC,平面DAC∩底面ABC=AC,
∴ DO⊥底面ABC.
(2)解:由条件易知DO⊥BO,BO⊥AC.
OA=OC=OD=2, OB=![]()
如图,以点O为坐标原点,OA为x轴, OB为y轴,OC为z轴建立空间直角坐标系.
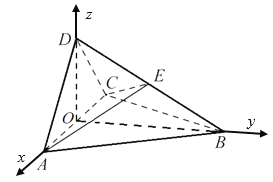
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面ADE的一个法向量为![]() ,
,
则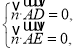 即
即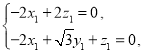
令![]() ,则
,则![]() ,所以
,所以![]() .
.
同理可得平面AEC的一个法向量![]() .
.
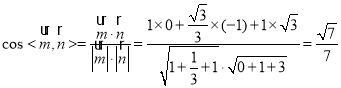 .
.
因为二面角D-AE-C的平面角为锐角,所以二面角D-AE-C的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
B.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”
”
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点F的直线交地物线于点A.B(其中点A在第一象限),交其准线l于点C,同时点F是AC的中点
的焦点F的直线交地物线于点A.B(其中点A在第一象限),交其准线l于点C,同时点F是AC的中点
(1)求直线AB的倾斜角;
(2)求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为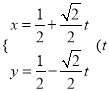 为参数), 椭圆C的参数方程为
为参数), 椭圆C的参数方程为![]() 为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2,
为参数)。在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(2, ![]()
(1)求椭圆C的直角坐标方程和点A在直角坐标系下的坐标
(2)直线l与椭圆C交于P,Q两点,求△APQ的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某歌舞团有![]() 名演员,他们编排了一些节目,每个节目都由四名演员同台表演.在一次演出中,他们发现:能适当安排若干个节目,使团中每两名演员都恰有一次在这次演出中同台表演。求
名演员,他们编排了一些节目,每个节目都由四名演员同台表演.在一次演出中,他们发现:能适当安排若干个节目,使团中每两名演员都恰有一次在这次演出中同台表演。求![]() 的最小值。
的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com