
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,两焦点分别为
,两焦点分别为![]() ,过
,过![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求弦长
两点,求弦长![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)求椭圆标准方程,一般利用待定系数法,即根据条件列两个独立方程:一是离心率![]() ,二是椭圆定义:
,二是椭圆定义:![]() 的周长为
的周长为![]() ,解方程组得
,解方程组得![]() ,
,![]() (2)涉及弦长问题,一般利用直线方程与椭圆方程联立方程组,结合韦达定理和弦长公式求弦长:设切线
(2)涉及弦长问题,一般利用直线方程与椭圆方程联立方程组,结合韦达定理和弦长公式求弦长:设切线![]() 的方程为
的方程为![]() ,则
,则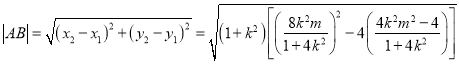 ,再根据直线与圆相切得
,再根据直线与圆相切得![]() ,即
,即![]() ,代入化简得
,代入化简得![]() ,最后利用基本不等式求最值
,最后利用基本不等式求最值
试题解析:(1)由题得:![]() ,........................1分
,........................1分
![]() ,...............................3分
,...............................3分
所以![]() .........................4分
.........................4分
又![]() ,所以
,所以![]() ,........................5分
,........................5分
即椭圆![]() 的方程为
的方程为![]() ....................6分
....................6分
(2)由题意知,![]() ,设切线
,设切线![]() 的方程为
的方程为![]() ,
,
由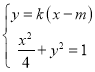 ,得
,得![]() ...............7分
...............7分
设![]() ,
,
则![]() .....................8分
.....................8分
![]() ,
,
由过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切得
相切得![]() ,即
,即![]() ,
,
所以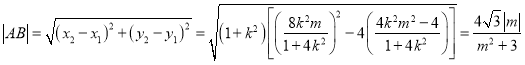 ....11分
....11分
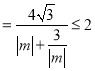 ,
,
当且仅当![]() 时,
时,![]() ,所以
,所以![]() 的最大值为2...................12分
的最大值为2...................12分


科目:高中数学 来源: 题型:
【题目】一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.
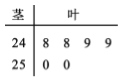
(Ⅰ)求这箱饮料的平均容量和容量的中位数;
(Ⅱ)如果从这箱饮料中随机取出2听饮用,求取到的2听饮料中至少有1听的容量为250ml的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)讨论函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)若![]() 且
且![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(Ⅲ)在(Ⅱ)的条件下,且![]() 取得最大值时,设
取得最大值时,设![]() ,且函数
,且函数![]() 有两个零点
有两个零点![]() ,求实数
,求实数![]() 的取值范围,并证明:
的取值范围,并证明: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com