
【题目】已知三棱柱ABC﹣A1B1C1的直观图和三视图如图所示,E是棱CC1上一点. 
(1)若CE=2EC1 , 求三棱锥E﹣ACB1的体积.
(2)若E是CC1的中点,求C到平面AEB1的距离.
【答案】
(1)解:由三视图得该三棱柱是侧棱长为2的直三棱柱,
底面ABC是以AB为斜边的等直角三角形,且AB=2,
∴AC⊥平面BB1C1C,BC⊥平面AA1C1C,
∵CE=2EC1,CC1=2,∴CE= ![]() ,
,
又AC= ![]() ,
,
∴三棱锥E﹣ACB1的体积:
![]() =
= ![]() =
= ![]()
(2)解:∵E是CC1的中点,CE=1,
∴AE=B1E= ![]() ,即△AEB1是等腰三角形,
,即△AEB1是等腰三角形,
∵AB1=2 ![]() ,∴△AEB1的高为
,∴△AEB1的高为 ![]() =1,
=1,
设C到平面AEB1的距离为d,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得d= ![]() .
.
∴C到平面AEB1的距离为 ![]() .
.

【解析】(1)由三视图得该三棱柱是侧棱长为2的直三棱柱,底面ABC是以AB为斜边的等直角三角形,且AB=2,三棱锥E﹣ACB1的体积 ![]() ,由此能求出结果.(2)设C到平面AEB1的距离为d,由
,由此能求出结果.(2)设C到平面AEB1的距离为d,由 ![]() =
= ![]() ,能求出C到平面AEB1的距离.
,能求出C到平面AEB1的距离.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 的方程化为普通方程,
的方程化为普通方程, ![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() ,
, ![]() 相交于
相交于![]() 两点,
两点, ![]() 的中点为
的中点为![]() ,过点
,过点![]() 做曲线
做曲线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
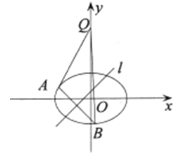
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某人的射击技术情况,在他的训练记录中抽取50次检验,他的命中环数如下:10,5,5,8,7,8,6,9,7,8,6,6,5,6,7,8,10,9,7,9,8,7,6,5,9,9,8,8,5,8,6,7,6,9,6,8,8,8,6,7,6,8,107,10,8,7,7,9,5
(1)列出频率分布表
(2)画出频率分布的直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(2x+ ![]() )(x∈R)的图象过点P(
)(x∈R)的图象过点P( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)已知f( ![]() +
+ ![]() )=
)= ![]() ,﹣
,﹣ ![]() <a<0,求cos(a﹣
<a<0,求cos(a﹣ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com