
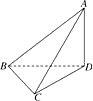
 如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为
如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
 (2013•临沂二模)如图,AD⊥平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为
(2013•临沂二模)如图,AD⊥平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,AD![]() 平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为
平面ABC,AD∥CE,AC=AD=AB=1,∠BAC=90°,凸多面体ABCED的体积为![]() ,F为BC的中点.
,F为BC的中点.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:平面BDE![]() 平面BCE.
平面BCE.

查看答案和解析>>
科目:高中数学 来源:2013年山东省临沂市高考数学二模试卷(文科)(解析版) 题型:解答题
 ,F为BC的中点.
,F为BC的中点.
查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:7 立体几何 质量检测(2)(解析版) 题型:解答题
 如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为 .
如图,AD⊥平面BCD,∠BCD=90°,AD=BC=CD=a,则二面角C-AB-D的大小为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com