�⣺����������֪

����Ϊa
2=b
2+c
2a
2=4��c
2=1������ԲC�ķ���

��3�֣�
������ֱ֪��l��б�ʴ��ڣ���ֱ��l����y=k��x-1������l��y�ύ��M��0��-k������ֱ��l����Բ��A��x
1��y
1����B��x
2��y
2��
��

�ã�3+4k
2��x
2-8k
2x+4k
2-12=0��
��

��6�֣�
����

��
�ࣨx
1��y
1��=�ˣ�1-x
1��-y
1����
��

��ͬ����

��8�֣�
��

���Ե�ֱ��l����б�DZ仯ʱ����+�̵�ֵΪ��ֵ
����10�֣�
����ֱ��lб�ʲ�����ʱ��ֱ��l��X�ᣬ��ABEDΪ���Σ��ɶԳ���֪��AE��BD�ཻFK���е�

���룬��ֱ��l����б�DZ仯ʱ��AE��BD�ཻ�ڶ���

��11�֣�
֤�����ɣ���֪A��x
1��y
1����B��x
2��y
2������D��4��y
1����E��4��y
2��
��ֱ��l����б�DZ仯ʱ������ֱ֤��AE������

��

��

ʱ��

=

=

���

��ֱ��l
AE�ϣ�ͬ����֤����

Ҳ��ֱ��l
BD�ϣ��൱m�仯ʱ��AE��BD�ཻ�ڶ���

����������������֪

����Ϊa
2=b
2+c
2a
2=4��c
2=1���ɴ��������ԲC�ķ��̣�
������ֱ��l����y=k��x-1������l��y�ύ��M��0��-1������ֱ��l����Բ��A��x
1��y
1����B��x
2��y
2������

�ã�3+4k
2��x
2-8k
2x+4k
2-12=0������Τ�ﶨ��������������ܹ��Ƶ�����ֱ��l����б�DZ仯ʱ����+�̵�ֵΪ��ֵ
��
����ֱ��lб�ʲ�����ʱ��ֱ��l��X�ᣬ��ABEDΪ���Σ��ɶԳ���֪��AE��BD�ཻFK���е�

���룬��ֱ��l����б�DZ仯ʱ��AE��BD�ཻ�ڶ���

��
֤������A��x
1��y
1����B��x
2��y
2����֪D��4��y
1����E��4��y
2������ֱ��l����б�DZ仯ʱ������ֱ֤��AE������

��֤��

Ҳ��ֱ��l
BD�ϣ����Ե�m�仯ʱ��AE��BD�ཻ�ڶ���

��
������������Ҫ����ֱ����Բ���ߵ��ۺ�Ӧ�������������漰���켣���̵���ֱ������Բ�����֪ʶ������ʱҪ�������Բ�������ʣ�ע������ؽ��еȼ�ת����

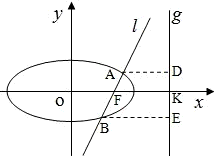 ֱ��l��y=k��x-1������֪��Բ
ֱ��l��y=k��x-1������֪��Բ �����㣨0��
�����㣨0�� ����������Ϊ
����������Ϊ ��������ԲC���ҽ���F��ֱ��l����Բ��A��B���㣬��A��F��B��ֱ��x=4�ϵ���Ӱ����Ϊ��D��K��E��
��������ԲC���ҽ���F��ֱ��l����Բ��A��B���㣬��A��F��B��ֱ��x=4�ϵ���Ӱ����Ϊ��D��K��E��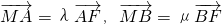 ����ֱ��l����б�DZ仯ʱ��̽���+�̵�ֵ�Ƿ�Ϊ��ֵ�����ǣ������+�̵�ֵ������˵�����ɣ�
����ֱ��l����б�DZ仯ʱ��̽���+�̵�ֵ�Ƿ�Ϊ��ֵ�����ǣ������+�̵�ֵ������˵�����ɣ� ����Ϊa2=b2+c2a2=4��c2=1������ԲC�ķ���
����Ϊa2=b2+c2a2=4��c2=1������ԲC�ķ��� ��3�֣�
��3�֣� �ã�3+4k2��x2-8k2x+4k2-12=0��
�ã�3+4k2��x2-8k2x+4k2-12=0�� ��6�֣�
��6�֣� ��
�� ��ͬ����
��ͬ���� ��8�֣�
��8�֣�
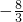 ����10�֣�
����10�֣�
 ��11�֣�
��11�֣� ��
��
 ʱ��
ʱ�� =
= =
= ���
��� ��ֱ��lAE�ϣ�ͬ����֤����
��ֱ��lAE�ϣ�ͬ����֤���� Ҳ��ֱ��lBD�ϣ��൱m�仯ʱ��AE��BD�ཻ�ڶ���
Ҳ��ֱ��lBD�ϣ��൱m�仯ʱ��AE��BD�ཻ�ڶ���
 ����Ϊa2=b2+c2a2=4��c2=1���ɴ��������ԲC�ķ��̣�
����Ϊa2=b2+c2a2=4��c2=1���ɴ��������ԲC�ķ��̣� �ã�3+4k2��x2-8k2x+4k2-12=0������Τ�ﶨ��������������ܹ��Ƶ�����ֱ��l����б�DZ仯ʱ����+�̵�ֵΪ��ֵ
�ã�3+4k2��x2-8k2x+4k2-12=0������Τ�ﶨ��������������ܹ��Ƶ�����ֱ��l����б�DZ仯ʱ����+�̵�ֵΪ��ֵ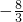 ��
�� ���룬��ֱ��l����б�DZ仯ʱ��AE��BD�ཻ�ڶ���
���룬��ֱ��l����б�DZ仯ʱ��AE��BD�ཻ�ڶ��� ��
�� ��֤��
��֤�� Ҳ��ֱ��lBD�ϣ����Ե�m�仯ʱ��AE��BD�ཻ�ڶ���
Ҳ��ֱ��lBD�ϣ����Ե�m�仯ʱ��AE��BD�ཻ�ڶ��� ��
��


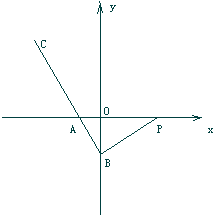 ��ͼ����ֱ֪��������PAB��ֱ�Ƕ���ΪB����P������Ϊ��3��0������B��y���ϣ���A��x��ĸ������ϣ���BA���ӳ�����ȡһ��C��ʹ
��ͼ����ֱ֪��������PAB��ֱ�Ƕ���ΪB����P������Ϊ��3��0������B��y���ϣ���A��x��ĸ������ϣ���BA���ӳ�����ȡһ��C��ʹ