
【题目】已知![]() .
.
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() ,证明:
,证明:![]() 。
。
【答案】(1)![]() 的取值范围是
的取值范围是![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)对函数进行求导,求出函数的单调性,可知函数的最小值,要想![]() 在
在![]() 恒成立,只需函数的最小值不小于零即可,解不等式,求出
恒成立,只需函数的最小值不小于零即可,解不等式,求出![]() 的取值范围。
的取值范围。
(2)通过(1)所知,函数的单调区间,由已知![]() ,可以得到两个变量的关系,不失一般性,设
,可以得到两个变量的关系,不失一般性,设![]() 可以得出
可以得出![]() ,要证
,要证![]() ,即
,即![]() ,则只需证
,则只需证![]() ,因为
,因为![]() ,则只需证
,则只需证![]() ,构造函数
,构造函数![]() ,对它求导,判断单调性,只要证明出
,对它求导,判断单调性,只要证明出![]() ,即可证明
,即可证明![]() 。
。
(1)![]() ,
,
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 取最小值
取最小值![]() 。
。
令![]() ,解得
,解得![]() ,故
,故![]() 的取值范围是
的取值范围是![]() 。
。
(2)由(1)知,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
不失一般性,设![]() ,则
,则![]() ,
,
要证![]() ,即
,即![]() ,则只需证
,则只需证![]() ,
,
因为![]() ,则只需证
,则只需证![]() ,
,
设![]() 。
。
则![]()
所以![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]()
又由题意得![]()
于是![]() ,即
,即![]()
因此![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() .沿
.沿![]() 将△
将△![]() 翻折到△
翻折到△![]() ,连接
,连接![]() ,得到如图的五棱锥
,得到如图的五棱锥![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点(异于点
上一动点(异于点![]() ),
),![]() 为线段
为线段![]() 上一动点,且
上一动点,且![]() .
.
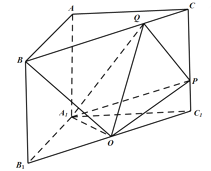
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—5:参数方程选讲]
在直角坐标系xoy中,曲线![]() 的参数方程是
的参数方程是 (t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
(t是参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两曲线交点为A、B,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】浦东一模之后的“大将” 洗心革面,再也没进过网吧,开始发奋学习. 2019年春节档非常热门的电影《流浪地球》引发了他的思考:假定地球(设为质点![]() ,地球半径忽略不计)借助原子发动机开始流浪的轨道是以木星(看作球体,其半径约为
,地球半径忽略不计)借助原子发动机开始流浪的轨道是以木星(看作球体,其半径约为![]() 万米)的中心
万米)的中心![]() 为右焦点的椭圆
为右焦点的椭圆![]() . 已知地球的近木星点
. 已知地球的近木星点![]() (轨道上离木星表面最近的点)到木星表面的距离为
(轨道上离木星表面最近的点)到木星表面的距离为![]() 万米,远木星点
万米,远木星点![]() (轨道上离木星表面最远的点)到木星表面的距离为
(轨道上离木星表面最远的点)到木星表面的距离为![]() 万米.
万米.

(1)求如图给定的坐标系下椭圆![]() 的标准方程;
的标准方程;
(2)若地球在流浪的过程中,由![]() 第一次逆时针流浪到与轨道中心
第一次逆时针流浪到与轨道中心![]() 的距离为
的距离为![]() 万米时(其中
万米时(其中![]() 分别为椭圆的长半轴、短半轴的长),由于木星引力,部分原子发动机突然失去了动力,此时地球向着木星方向开始变轨(如图所示),假定地球变轨后的轨道为一条直线
分别为椭圆的长半轴、短半轴的长),由于木星引力,部分原子发动机突然失去了动力,此时地球向着木星方向开始变轨(如图所示),假定地球变轨后的轨道为一条直线![]() ,称该直线的斜率
,称该直线的斜率![]() 为“变轨系数”. 求“变轨系数”
为“变轨系数”. 求“变轨系数”![]() 的取值范围,使地球与木星不会发生碰撞. (精确到小数点后一位)
的取值范围,使地球与木星不会发生碰撞. (精确到小数点后一位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com