
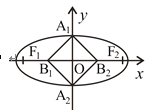
【题目】如图,已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,短轴的两端点分别为
,短轴的两端点分别为![]() ,
,![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,且四边形
,且四边形![]() 是面积为8的矩形.
是面积为8的矩形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ; (2)
; (2)![]() 或
或![]() .
.
【解析】
(I)通过矩形![]() 的面积和对角线长相等列方程组,结合
的面积和对角线长相等列方程组,结合![]() ,解得
,解得![]() 的值,从而求得椭圆方程.(II)当直线
的值,从而求得椭圆方程.(II)当直线![]() 的斜率不存在时,直接得出直线
的斜率不存在时,直接得出直线![]() 的方程,代入椭圆方程求得
的方程,代入椭圆方程求得![]() 两点的坐标,代入
两点的坐标,代入![]() 验证出不符合题意.当直线
验证出不符合题意.当直线![]() 的斜率存在时,设出直线
的斜率存在时,设出直线![]() 的方程,联立直线的方程和椭圆的方程,化简后写出韦达定理,将坐标代入
的方程,联立直线的方程和椭圆的方程,化简后写出韦达定理,将坐标代入![]() ,解方程求得直线
,解方程求得直线![]() 的斜率,由此求得直线
的斜率,由此求得直线![]() 的方程.
的方程.
(I)在矩形![]() 中,
中,![]()
所以四边形![]() 是正方形,所以
是正方形,所以
又![]()
![]() ,
,
∴椭圆C的方程为![]() .
.
(II)由(I)可知![]() ,
,
1)当直线l的斜率不存在时,l的方程为x=-2,
由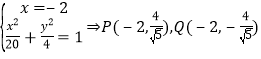
![]()
![]()
∴l:x=-2不满足题意.
2)当l的斜率为k时,设l的方程为![]() ,
,![]()
由
则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
综上所述,直线l的方程为![]() 或
或![]()


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.
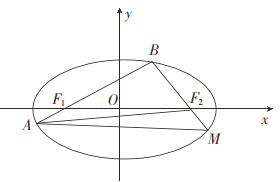
(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的长轴长与焦距之比为
的长轴长与焦距之比为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)当![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积;
的面积;
(2)当线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距最小时,求直线
轴上的截距最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直接坐标系![]() 中,直线l的方程为x-y+4=0,曲线C的参数方程为
中,直线l的方程为x-y+4=0,曲线C的参数方程为![]() .
.
(I)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,![]() ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+![]() -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,E,F分别为A1C1和BC的中点,M,N分别为A1B和A1C的中点.求证:
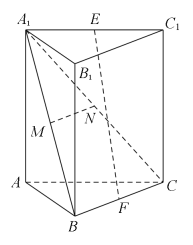
(1)MN∥平面ABC;
(2)EF∥平面AA1B1B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(﹣1,3),B(3,3)两点,且圆心C在直线x﹣y+1=0上.
(1)求圆C的方程;
(2)求经过圆上一点A(﹣1,3)的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在4件产品中,有一等品2件,二等品1件(一等品与二等品都是正品),次品1件,现从中任取2件,则下列说法正确的是( )
A.两件都是一等品的概率是![]()
B.两件中有1件是次品的概率是![]()
C.两件都是正品的概率是![]()
D.两件中至少有1件是一等品的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率等于![]() .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com