
【题目】三棱柱![]() 中,侧棱与底面垂直,
中,侧棱与底面垂直,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
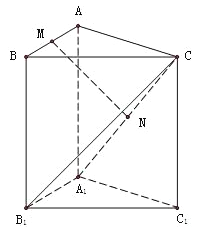
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】⑴见解析![]() ⑵见解析 ⑶
⑵见解析 ⑶![]()
【解析】
试题(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证往往需要利用平几知识,如本题就利用三角形中位线定理得![]() (2)利用空间向量证明线面垂直,实际就是以算代证,即先求平面的一个法向量,再利用
(2)利用空间向量证明线面垂直,实际就是以算代证,即先求平面的一个法向量,再利用![]() 与法向量关系关系求证(3)求二面角的大小,一般利用空间向量的数量积求解,先建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出各面的法向量,利用向量数量积求法向量的夹角余弦值,最后根据二面角与法向量夹角之间关系求值.
与法向量关系关系求证(3)求二面角的大小,一般利用空间向量的数量积求解,先建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出各面的法向量,利用向量数量积求法向量的夹角余弦值,最后根据二面角与法向量夹角之间关系求值.
试题解析:(1)连接![]() ,
,![]() ,
,
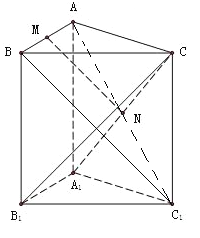
在![]() 中,∵
中,∵![]() 是
是![]() 中点,∴
中点,∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
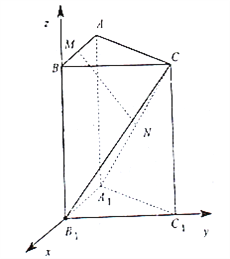
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
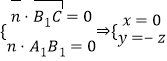 ,
,
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() .
.
(3)设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,
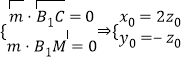 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
所求二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点.求异面直线A1E与GF所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定圆![]() ,定直线
,定直线![]() ,过
,过![]() 的一条动直线
的一条动直线![]() 与直线
与直线![]() 相交于
相交于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
, ![]() 两点,
两点, ![]() 是
是![]() 中点.
中点.
(Ⅰ)当![]() 与
与![]() 垂直时,求证:
垂直时,求证: ![]() 过圆心
过圆心![]() .
.
(Ⅱ)当![]() ,求直线
,求直线![]() 的方程.
的方程.
(Ⅲ)设![]() ,试问
,试问![]() 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出![]() 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为 ![]() ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com