
【题目】在数列{an}中,a1=2,a2=4,且当n≥2时,an2=an-1an+1,![]() ;
;
(1)求数列{an}的通项公式an;
(2)若bn=(2n-1)an,求数列{bn}的前n项和Sn.
【答案】(1)an=2n; (2)Sn=6+(2n-3)×2n+1.
【解析】
(1)由当n≥2时,an2=an-1an+1可判断数列{an}为等比数列,再结合a1=2,a2=4即可求解;
(2)由(1)得bn=(2n-1)2n,再采用错位相减法即可求得;
(1)∵当n≥2时,an2=an-1an+1,∴数列{an}是等比数列,
又∵a1=2,a2=4,∴公比a=![]() =2,
=2,
∴数列{an}是首项、公比均为2的等比数列,∴其通项公式an=2n;
(2)由(1)可知bn=(2n-1)an=(2n-1)2n,
则Sn=1×2+3×22+5×23+…+(2n-1)×2n,
2Sn=1×22+3×23+…+(2n-3)×2n+(2n-1)×2n+1,
两式相减,得:-Sn=2+2×22+2×23+…+2×2n-(2n-1)×2n+1
=2+2×![]() -(2n-1)×2n+1=-6-(2n-3)×2n+1,
-(2n-1)×2n+1=-6-(2n-3)×2n+1,
∴Sn=6+(2n-3)×2n+1.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 且
且![]() .
.
(1)若![]() 为整数,且
为整数,且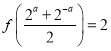 ,试确定一个满足条件的
,试确定一个满足条件的![]() 的值;
的值;
(2)设![]() 的反函数为
的反函数为![]() ,若
,若![]() ,试确定
,试确定![]() 的取值范围;
的取值范围;
(3)若![]() ,此时
,此时![]() 的反函数为
的反函数为![]() ,令
,令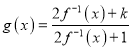 ,若对一切实数
,若对一切实数![]() ,
,![]() ,
,![]() ,不等式
,不等式![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在D上的函数,若对任何实数α∈(0,1)以及D中的任意两数x1,x2,恒有f(αx1+(1﹣α)x2)≤αf(x1)+(1﹣α)f(x2),则称f(x)为定义在D上的C函数.
(1)试判断函数f1(x)=x2,![]() 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;
(2)若f(x)是定义域为![]() 的函数且最小正周期为T,试证明f(x)不是R上的C函数.
的函数且最小正周期为T,试证明f(x)不是R上的C函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)若对任意![]() ,
,![]() 且
且![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)在第(1)问求出的实数![]() 的范围内,若存在一个与
的范围内,若存在一个与![]() 有关的负数
有关的负数![]() ,使得对任意
,使得对任意![]() 时
时![]() 恒成立,求
恒成立,求![]() 的最小值及相应的
的最小值及相应的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某电商2019年12月1日至12月16日的日销售量(单位:件)统计图,销量小于100称为该商品滞销,销量大于200称为该商品畅销,则下列关于该商品在这16天的销量的说法不正确的是( )

A.该商品出现过连续4天畅销
B.该商品畅销的频率为0.5
C.相邻两天该商品销量之差的最大值为195
D.该商品销量的平均数小于200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]()
(1)求圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为8,求直线
截得的弦长为8,求直线![]() 的方程;
的方程;
(3)当![]() 取何值时,直线
取何值时,直线![]() 与圆
与圆![]() 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知顶点![]() ,
,![]() ,动点
,动点![]() 分别在
分别在![]() 轴,
轴,![]() 轴上移动,延长
轴上移动,延长![]() 至点
至点![]() ,使得
,使得![]() ,且
,且![]() .
.
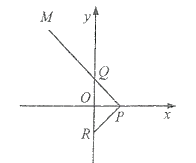
(1)求动点![]() 的轨迹
的轨迹![]() ;
;
(2)过点![]() 分别作直线
分别作直线![]() 交曲线于
交曲线于![]() 两点,若直线
两点,若直线![]() 的倾斜角互补,证明:直线的斜率为定值;
的倾斜角互补,证明:直线的斜率为定值;
(3)过点![]() 分别作直线
分别作直线![]() 交曲线于
交曲线于![]() 两点,若
两点,若![]() ,直线
,直线![]() 是否经过定点?若是,求出该定点,若不是,说明理由.
是否经过定点?若是,求出该定点,若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com