
【题目】在公差为d的等差数列{an}中,已知a1=10,5a1a3=(2a2+2)2 .
(1)求d和an的值;
(2)若d<0,求|a1|+|a2|+|a3|+…+|a2021|的值.
【答案】
(1)解:∵a1=10,5a1a3=(2a2+2)2,
∴50(10+2d)=4(10+d+1)2,
即d2﹣3d﹣4=0,解得d=﹣1或d=4.
故an=﹣n+11或an=4n+6.
(2)解:由题知d=﹣1,an=﹣n+11,则当n≤11时,an≥0,
当n>11时,an<0,
则|a1|+|a2|+|a3|+…+|a2021|=(a1+…+a11)﹣(a12+…+a2021)
=2(a1+…+a11)﹣(a1+a2…+a2021)
=2× ![]() ﹣
﹣ ![]()
=2021110
【解析】(1)利用等差数列的通项公式列出方程解出公差,代入通项公式即可;(2)利用通项公式判断{an}的非负项项数,使用求和公式计算.
【考点精析】本题主要考查了等差数列的前n项和公式和数列的前n项和的相关知识点,需要掌握前n项和公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系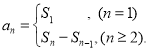 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( ) 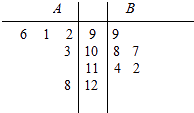
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,DA⊥AB,
 DE=1,EC=
DE=1,EC=![]() ,EA=2,
,EA=2,
∠ADC=![]() ,∠BEC=
,∠BEC=![]() .
.
(Ⅰ)求sin∠CED的值;
(Ⅱ)求BE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE, ![]() ,F为线段DE上的一点.
,F为线段DE上的一点. 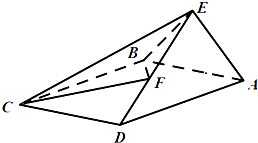
(1)求证:平面AED⊥平面ABCD;
(2)若二面角E﹣BC﹣F与二面角F﹣BC﹣D的大小相等,求DF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且点P为AD的中点,点Q为SB的中点.

(1)求证:CD⊥平面SAD.
(2)求证:PQ∥平面SCD.
(3)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
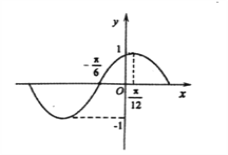
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C满足
中,角A,B,C满足![]() ,且其外接圆的半径R=2,求
,且其外接圆的半径R=2,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,一个动圆截直线![]() 和
和![]() 所得的弦长分别为8,4.
所得的弦长分别为8,4.
(1)求动圆圆心的轨迹方程![]() ;
;
(2)在轨迹![]() 上是否存在这样的点:它到点
上是否存在这样的点:它到点![]() 的距离等于到点
的距离等于到点![]() 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( ) 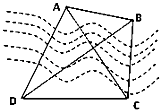
A.![]() m
m
B.200 ![]() m
m
C.100 ![]() m
m
D.数据不够,无法计算
查看答案和解析>>
科目:高中数学 来源: 题型:
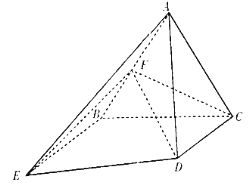
【题目】如图所示,正三角形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为30°,求三棱锥
所成的角为30°,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com