
【题目】已知函数![]() .
.
(1)讨论f(x)的单调性;
(2)证明:当﹣1<a<0时,f(x)存在唯一的零点x0,且x0随着a的增大而增大.
【答案】(1)答案不唯一,具体见解析(2)证明见解析
【解析】
(1)先求得函数![]() 的定义域,求得函数的导函数
的定义域,求得函数的导函数![]() ,对
,对![]() 分成
分成![]() 等四种情况进行分类讨论,由此求得
等四种情况进行分类讨论,由此求得![]() 的单调区间.
的单调区间.
(2)![]() 时,由(1)得到
时,由(1)得到![]() 的单调性,结合零点存在性定理判断出
的单调性,结合零点存在性定理判断出![]() 存在唯一零点
存在唯一零点![]() .令
.令![]() ,由此对
,由此对![]() 分离常数,利用导数证得
分离常数,利用导数证得![]() 随
随![]() 增大而增大.
增大而增大.
(1)f(x)的定义域为(0,+∞);
![]() ;
;
①当a=0时,![]() ,则f(x)在(0,+∞)上单调递减;
,则f(x)在(0,+∞)上单调递减;
②当a>0时,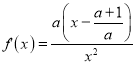 ,而
,而![]() ;
;
则f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
③当﹣1≤a<0时,f′(x)<0,则f(x)在(0,+∞)上单调递减;
④当a<﹣1时,f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
综上,当a<﹣1时,f(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当﹣1≤a≤0时,f′(x)<0,则f(x)在(0,+∞)上单调递减;
当a>0时,f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2)由(1)得当﹣1<a<0时,f(x)在(0,+∞)上单调递减;
∴f(x)至多有一个零点;
又﹣1<a<0;
∴![]() ,f(1)=a+1>0,
,f(1)=a+1>0,![]() ;
;
令g(x)=x﹣1﹣lnx,则![]() ;
;
∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
g(x)≥g(1)=0,即x﹣1﹣lnx≥0,当且仅当x=1时取等号;
∴![]() ;
;
∴f(x)存在唯一得零点![]() ;
;
由f(x0)=0,得![]() ,即
,即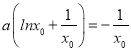 ;
;
∵x0∈(1,+∞),![]() ;
;
∴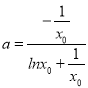 ,即a是x0的函数;
,即a是x0的函数;
设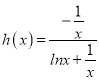 ,x∈(1,+∞),则
,x∈(1,+∞),则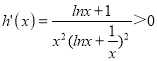 ;
;
∴h(x)为(1,+∞)上的增函数;
∴![]() 随
随![]() 增大而增大,反之亦成立.
增大而增大,反之亦成立.
∴x0随着a的增大而增大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的对称中心为原点
的对称中心为原点![]() ,焦点在
,焦点在![]() 轴上,焦距为
轴上,焦距为![]() ,点
,点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆![]() 的方程;
的方程;
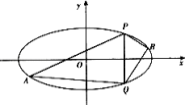
(2)直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 点位于第一象限,
点位于第一象限,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当点
两侧的动点.当点![]() 运动时,满足
运动时,满足![]() ,问直线
,问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南北朝时,张邱建写了一部算经,即《张邱建算经》,在这本算经中,张邱建对等差数列的研究做出了一定的贡献.例如算经中有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给”,则某一等人比其下一等人多得________斤金.(不作近似计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在![]() 上的单调函数,且对任意的x∈
上的单调函数,且对任意的x∈![]() 都有
都有![]() ,则方程
,则方程![]() 的一个根所在的区间是( )
的一个根所在的区间是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)当![]() 时,写出直线l的普通方程及曲线C的直角坐标方程;
时,写出直线l的普通方程及曲线C的直角坐标方程;
(2)已知点![]() ,设直线l与曲线C交于A,B两点,试确定
,设直线l与曲线C交于A,B两点,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为矩形,且AB=![]() ,BC=1,E,F分别为AB,PC中点.
,BC=1,E,F分别为AB,PC中点.

(1)求证:EF∥平面PAD;
(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下列四个结论:
有下列四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最小正周期为
的最小正周期为![]() ;③
;③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的值域为
的值域为![]() .
.
上述结论中,正确的为( )
A.③④B.②④C.①③D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com