
【题目】已知![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,记
时,记![]() ,已知
,已知![]() 有三个极值点,求
有三个极值点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时,![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;(Ⅱ)
单调递减;(Ⅱ)![]() ,且
,且![]() .
.
【解析】
试题分析:(Ⅰ)由![]() ,分
,分![]() 、
、![]() 讨论;(Ⅱ)由已知
讨论;(Ⅱ)由已知![]() ,
,
则![]() ,若
,若![]() 有三个极值点,则
有三个极值点,则![]() 有两个不为
有两个不为![]() 且不为1的相异实根,令
且不为1的相异实根,令![]() ,由函数值分布值,若
,由函数值分布值,若![]() 有两个相异实根,则
有两个相异实根,则![]() ,∴
,∴![]() ,又
,又![]() 及
及![]() 时,
时,![]() ,故
,故![]() 的取值范围为
的取值范围为![]() ,且
,且![]() .
.
试题解析:(Ⅰ)∵![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
所以,当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递增.
单调递增.
当![]() 时,令
时,令![]() ,∴
,∴![]() ,
,
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递增.
单调递增.
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递减.
单调递减.
(Ⅱ)当![]() 时,
时,![]() .
.
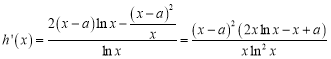 .
.
∵![]() 有三个极值点,∴
有三个极值点,∴![]() 有三个相异的实根.
有三个相异的实根.
所以![]() 有两个不为
有两个不为![]() 且不为1的相异实根.
且不为1的相异实根.
令![]() ,令
,令![]() ,∴
,∴![]() ,列表得
,列表得
|
|
|
|
|
| - | 0 | + | + |
| 单调递减 | 单调递增 | 单调递增 |
![]() 时,
时,![]() ,
,![]() 时,
时,![]()
大致图象为

若![]() 有两个相异实根,则
有两个相异实根,则![]() ,∴
,∴![]() ,
,
若![]() ,则
,则![]() ,因为
,因为![]() 的根不为
的根不为![]() ,所以
,所以![]() .
.
若![]() ,则
,则![]() ,因为
,因为![]() 的根不为1,所以
的根不为1,所以![]() .
.
综上![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
【题目】某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤ x ≤80时,每天售出的件数为P=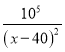 ,每天获得的利润为y(元)
,每天获得的利润为y(元)
(1)写出关于x的函数y的表达式;
(2)若想每天获得的利润最多,问售价应定为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
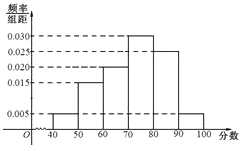
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入![]() 万元,以后每年投入将比上年减少
万元,以后每年投入将比上年减少![]() .本年度当地旅游业收入估计为
.本年度当地旅游业收入估计为![]() 万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加![]() .
.
(Ⅰ)设![]() 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为![]() 万元,旅游业总收入为
万元,旅游业总收入为![]() 万元.写出
万元.写出![]() 的表达式;
的表达式;
(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
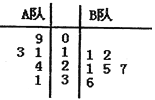
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com