
【题目】如图,在直角梯形![]() 中,E,F分别为AB的三等分点,
中,E,F分别为AB的三等分点,![]() ,
,![]() ,
,![]() ,
,![]() 若沿着FG,ED折叠使得点A,B重合,如图2所示,连结GC,BD
若沿着FG,ED折叠使得点A,B重合,如图2所示,连结GC,BD
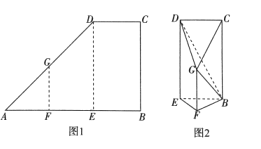
(1)求证:平面![]() 平面BCDE;
平面BCDE;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)取BD,BE的中点分别为O,M,连结GO,OM,MF,先证四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ,再证
,再证![]() 平面
平面![]() ,因此
,因此![]() 平面
平面![]() ,进而可得平面
,进而可得平面![]() 平面
平面![]() ;
;
(2)以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,求出各点坐标,求得平面CDG和平面CBG的法向量,进而求得二面角
轴,建立空间直角坐标系,求出各点坐标,求得平面CDG和平面CBG的法向量,进而求得二面角![]() 的余弦值.
的余弦值.
(1)如图,取BD,BE的中点分别为O,M,连结GO,OM,MF,

![]()
![]() ,
,![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
故四边形![]() 为平行四边形,
为平行四边形,
故![]() ,
,
因为M为EB的中点,三角形![]() 为等边三角形,故
为等边三角形,故![]() ,
,
因为平面![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() ;
;
(2)建立如图所示的空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面CDG的法向量为![]() ,则
,则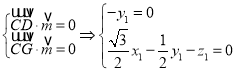 ,
,
取![]() ,得:
,得:![]() ,
,
同理得出平面CBG的法向量![]() ,
,
![]()
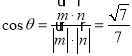 ,
,
所以二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】坐标系与参数方程:在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上
上
(Ⅰ)求![]() 的值和直线
的值和直线![]() 的直角坐标方程及
的直角坐标方程及![]() 的参数方程;
的参数方程;
(Ⅱ)已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),直线
为参数),直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
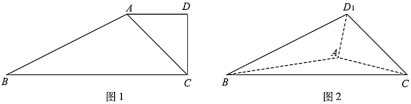
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与x轴的交点为H,点F为抛物线的焦点,点P在抛物线上且
的准线与x轴的交点为H,点F为抛物线的焦点,点P在抛物线上且![]() ,当k最大时,点P恰好在以H,F为焦点的双曲线上,则k的最大值为_____,此时该双曲线的离心率为_____.
,当k最大时,点P恰好在以H,F为焦点的双曲线上,则k的最大值为_____,此时该双曲线的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】渭南市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:渭南城区所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人.违反者将被处以
条规定:渭南城区所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人.违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.下表是渭南市一主干路段,监控设备所抓拍的
分的行政处罚.下表是渭南市一主干路段,监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路![]() 月份的不“礼让斑马线”违章驾驶员人数;
月份的不“礼让斑马线”违章驾驶员人数;
(3)若从表中![]() 、
、![]() 月份分别抽取
月份分别抽取![]() 人和
人和![]() 人,然后再从中任选
人,然后再从中任选![]() 人进行交规调查,求拍到的两人恰好来自同一月份的概率.
人进行交规调查,求拍到的两人恰好来自同一月份的概率.
参考公式: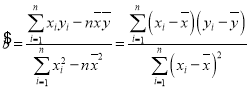 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种细菌的适宜生长温度为12℃~27℃,为了研究该种细菌的繁殖数量![]() (单位:个)随温度
(单位:个)随温度![]() (单位:℃)变化的规律,收集数据如下:
(单位:℃)变化的规律,收集数据如下:
温度 | 14 | 16 | 18 | 20 | 22 | 24 | 26 |
繁殖数量 | 25 | 30 | 38 | 50 | 66 | 120 | 218 |
对数据进行初步处理后,得到了一些统计量的值,如表所示:
|
|
|
|
|
|
|
20 | 78 | 4.1 | 112 | 3.8 | 1590 | 20.5 |
其中![]() ,
,![]() .
.
(1)请绘出![]() 关于
关于![]() 的散点图,并根据散点图判断
的散点图,并根据散点图判断![]() 与
与![]() 哪一个更适合作为该种细菌的繁殖数量
哪一个更适合作为该种细菌的繁殖数量![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表格数据,建立![]() 关于
关于![]() 的回归方程(结果精确到0.1);
的回归方程(结果精确到0.1);
(3)当温度为27℃时,该种细菌的繁殖数量的预报值为多少?
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二成估计分别为
的斜率和截距的最小二成估计分别为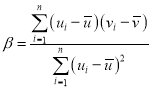 ,
,![]() ,参考数据:
,参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com