
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如下表所示:

(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程![]() ,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式: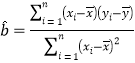 ,
,![]()
【答案】(1)![]() (2)正相关,回归直线的方程为
(2)正相关,回归直线的方程为![]() ,估计值为42
,估计值为42
【解析】试题分析:(1)利用枚举法确定从这5年中任意抽取两年,所有的事件个数:10;再从中确定至少有1年多于20个的事件数:7,最后根据古典概型概率公式求概率,(2)先计算平均数![]() ,
,![]() ,再代入公式求
,再代入公式求![]() ,根据
,根据![]() 值的正负确定正相关还是负相关;利用
值的正负确定正相关还是负相关;利用![]() 求
求![]() ,最后求自变量为2019时对应函数值
,最后求自变量为2019时对应函数值
试题解析:解:(Ⅰ)从这5年中任意抽取两年,所有的事件有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种,
共10种,
至少有1年多于20人的事件有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共7种,
共7种,
则至少有1年多于20人的概率为![]() .
.
(Ⅱ)由已知数据得![]() ,
,![]() ,
,
![]()
![]()
![]() ;
;
![]()
![]() ;
;
所以 ,
,![]()
所以是正相关,回归直线的方程为![]()
则第2019年的估计值为![]()


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在PD上.
,PA=2,点M在PD上. 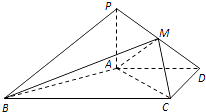
(1)求证:AB⊥PC
(2)若二面角M﹣AC﹣D的大小为45°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s ![]() 和s
和s ![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率. 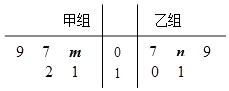
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax2-e2x.
(1)若曲线y=f(x)在点(2,f(2))处的切线平行于x轴,求函数f(x)的单调区间;
(2)若x>0时,总有f(x)>-e2x,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com