
【题目】已知函数f(x)=ex+ax2-e2x.
(1)若曲线y=f(x)在点(2,f(2))处的切线平行于x轴,求函数f(x)的单调区间;
(2)若x>0时,总有f(x)>-e2x,求实数a的取值范围.
【答案】(1) f(x)在(-∞,2)上单调递减;f(x)在(2,+∞)上单调递增;(2) ![]()
【解析】试题分析:
(1)由导函数与斜率的关系可得![]() ,则函数f(x)在(-∞,2)上单调递减;f(x)在(2,+∞)上单调递增;
,则函数f(x)在(-∞,2)上单调递减;f(x)在(2,+∞)上单调递增;
(2)分离系数后构造新函数![]() ,结合新函数的特征可得 实数a的取值范围是
,结合新函数的特征可得 实数a的取值范围是 .
.
试题解析:
(1)由f′(x)=ex+2ax-e2,得
y=f(x)在点(2,f(2))处的切线斜率k=4a=0,则a=0.
此时f(x)=ex-e2x,f′(x)=ex-e2.
由f′(x)=0,得x=2.
当x∈(-∞,2)时,f′(x)<0,f(x)在(-∞,2)上单调递减;
当x∈(2,+∞)时, f′(x)>0,f(x)在(2,+∞)上单调递增.
(2)由f(x)>-e2x,得a>-![]() .设g(x)=-
.设g(x)=-![]() ,x>0,则g′(x)=
,x>0,则g′(x)=![]() .
.
∴当0<x<2时,g′(x)>0,g(x)在(0,2)上单调递增;
当x>2时,g′(x)<0,g(x)在(2,+∞)上单调递减.
∴g(x)≤g(2)=-![]() .因此实数a的取值范围为
.因此实数a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如下表所示:

(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程![]() ,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式: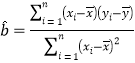 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
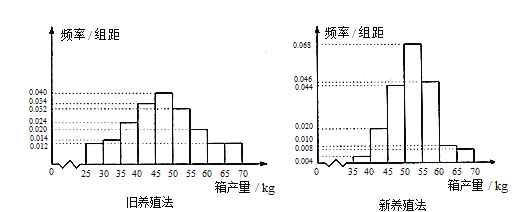
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: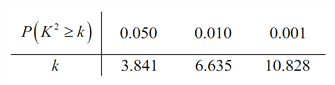 ,
, 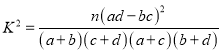
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾,郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动I级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |

(1)请在图中完成被调查人员年龄的频率分布直方图;
(2)若从年龄在![]() ,
, ![]() 两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为
两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=(x﹣a)2+|x﹣a|﹣a(a﹣1).
(1)若f(0)≤1,求a的取值范围;
(2)求f(x)在R上的单调区间(无需使用定义严格证明,但必须有一定的推理过程);
(3)当a>2时,求函数g(x)=f(x)+|x|在R上的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com