
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量t(条)是售价x(元)(x∈Z+)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(x∈Z+)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润﹣总管理、仓储等费用)?
【答案】
(1)解:设t=kx+b,∴ ![]() ,解得k=﹣2,b=70,∴t=70﹣2x.
,解得k=﹣2,b=70,∴t=70﹣2x.
y=(x﹣10)t=(x﹣10)(70﹣2x)=﹣2x2+90x﹣700,
∵ ![]() ,∴围巾定价为22元或23元时,每日的利润最高
,∴围巾定价为22元或23元时,每日的利润最高
(2)解:设售价x(元)时总利润为z(元),
∴z=2000(x﹣10)﹣200 ![]()
=2000(25﹣((35﹣x)+ ![]() ))≤2000(25﹣
))≤2000(25﹣ ![]() )=10000元.
)=10000元.
当35﹣x= ![]() 时,即x=25时,取得等号.
时,即x=25时,取得等号.
∴小张的这批围巾定价为25元时,这批围巾的总利润最高
【解析】(1)根据题意先求出销售量t与售价x之间的关系式,再利用毛利润为每日卖出商品的进货价与销售价之间的差价,确定毛利润y(元)关于售价x(元)(x∈Z+)的函数关系式,利用二次函数求最值的方法可求;(2)根据总利润=总毛利润﹣总管理、仓储等费用,构建函数关系,利用基本不等式可求最值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的上下顶点分别为
的上下顶点分别为![]() ,且点
,且点![]() .
. ![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且
的左、右焦点,且![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)点![]() 是椭圆上异于
是椭圆上异于![]() ,
, ![]() 的任意一点,过点
的任意一点,过点![]() 作
作![]() 轴于
轴于![]() ,
, ![]() 为线段
为线段![]()
的中点.直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为坐标原点.求
为坐标原点.求
![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,若存在常数
,若存在常数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() ,则称
,则称![]() 为有界集合,同时称
为有界集合,同时称![]() 为集合
为集合![]() 的上界.
的上界.
(1)设![]() 、
、![]() ,试判断
,试判断![]() 、
、![]() 是否为有界集合,并说明理由;
是否为有界集合,并说明理由;
(2)已知![]() ,记
,记![]() (
(![]() ).若
).若![]() ,
,
![]() ,且
,且![]() 为有界集合,求
为有界集合,求![]() 的值及
的值及![]() 的取值范围;
的取值范围;
(3)设![]() 均为正数,将
均为正数,将![]() 中的最小数记为
中的最小数记为![]() .是否存在正数
.是否存在正数![]() ,使得
,使得![]() 为有界集合
为有界集合![]() ,
, ![]() 均为正数
均为正数![]() 的上界,若存在,试求
的上界,若存在,试求![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式 ![]() 的解集为B,集合
的解集为B,集合 ![]() ,集合D={x|m+1≤x<2m﹣1}(m>0)
,集合D={x|m+1≤x<2m﹣1}(m>0)
(1)若A∪B=B,求实数a的取值范围;
(2)若DC,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数y=f(x)的局部对称点.
(1)若a、b∈R且a≠0,证明:函数f(x)=ax2+bx﹣a必有局部对称点;
(2)若函数f(x)=2x+c在定义域[﹣1,2]内有局部对称点,求实数c的取值范围;
(3)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=![]() ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点.
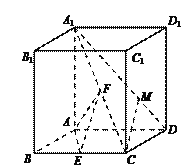
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, ![]() .若CM∥平面AEF,求实数λ的值.
.若CM∥平面AEF,求实数λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com