
【题目】已知函数![]() ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 有两个零点,试求
有两个零点,试求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]()
【解析】试题分析:(1)根据导数的几何意义得到![]() ,
, ![]() ,根据这两点可以写出切线方程。(2)对函数
,根据这两点可以写出切线方程。(2)对函数![]() 进行单调性的研究,分
进行单调性的研究,分![]() ,
, ![]() ,
, ![]() ,三种情况讨论单调性,研究函数的图像变换趋势,得到参数方位。(3)原不等式等价于
,三种情况讨论单调性,研究函数的图像变换趋势,得到参数方位。(3)原不等式等价于![]() 恒成立,对右侧函数研究单调性得最值即可。
恒成立,对右侧函数研究单调性得最值即可。
解析:
(Ⅰ)当![]() 时,
时, ![]() .
.![]() ,
, ![]() .
.
所以函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)函数![]() 的定义域为
的定义域为![]() ,由已知得
,由已知得![]() .
.
①当![]() 时,函数
时,函数![]() 只有一个零点;
只有一个零点;
②当![]() ,因为
,因为![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增. 又
上单调递增. 又![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,
, ![]() 所以
所以![]() ,所以
,所以![]()
取![]() ,显然
,显然![]() 且
且![]()
所以![]() ,
, ![]() .
.
由零点存在性定理及函数的单调性知,函数有两个零点.
③当![]() 时,由
时,由![]() ,得
,得![]() ,或
,或![]() .
.
![]() 当
当![]() ,则
,则![]() .当
.当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:

注意到![]() ,所以函数
,所以函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
![]() 当
当![]() ,则
,则![]() ,
, ![]() 在
在![]() 单调递增,函数
单调递增,函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
若![]() ,则
,则![]() .当
.当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
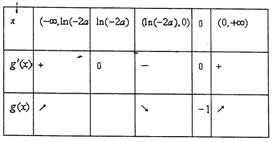
注意到当![]() ,
, ![]() 时,
时, ![]() ,
, ![]() ,所以函数
,所以函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
综上, ![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,
时, ![]() ,
,
即![]() ,令
,令![]() ,则
,则![]()
令![]() ,则
,则![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增
单调递增
又![]() ,
, ![]() ,所以,当
,所以,当![]() 时,
时, ![]() ,即
,即![]() ,
,
所以![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,即
,即![]() ,
,
所以![]() 单调递增,所以
单调递增,所以![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
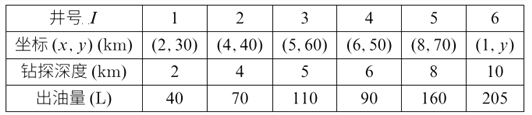
【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:
(参考公式和计算结果:
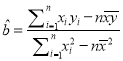 ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() 的值,并估计
的值,并估计![]() 的预报值.
的预报值.
(2)现准备勘探新井![]() ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的![]() ,
, ![]() 的值(
的值(![]() ,
, ![]() 精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的![]() ,
, ![]() ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,给出以下命题:

①异面直线C1P与B1C所成的角为定值;
②二面角P-BC1-D的大小为定值;
③三棱锥D-BPC1的体积为定值;
④异面直线A1P与BC1间的距离为定值.
其中真命题的个数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)点M在线段PC上,PM=tPC,试确定实数t的值,使得PA∥平面MQB.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩![]() 分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
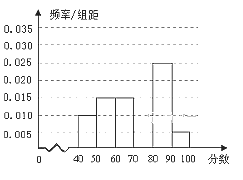
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试的平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为![]() ,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量
,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 且与
且与![]() 轴垂直的弦长为3.
轴垂直的弦长为3.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值,若存在,请求出
为定值,若存在,请求出![]() 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆C1: ![]() 和椭圆C2:
和椭圆C2: ![]() 的焦点相同且a1>a2.给出如下四个结论:
的焦点相同且a1>a2.给出如下四个结论:
①椭圆C1和椭圆C2一定没有公共点;
②![]() ;
;
③![]() ;
;
④a1-a2<b1-b2.
其中,所有正确结论的序号是( )
A. ②③④ B. ①③④
C. ①②④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率.
(1)求该市所有县乡中学教师流失数不低于8的概率;
(2)若从上述50所县乡中学中流失教师数不低于9的县乡学校中任取两所调查回访,了解其中原因,求这两所学校的教师流失数都是10的概率.
流失教师数 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 2 | 4 | 11 | 16 | 12 | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com