
【题目】已知距离为![]() 的
的![]() 、
、![]() 两点在直线
两点在直线![]() 的同侧,且
的同侧,且![]() 、
、![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 、
、![]() .问能否作出经过
.问能否作出经过![]() 、
、![]() 两点且与直线
两点且与直线![]() 相切的圆?若能,请写出作法,画图并求出圆的半径;若不能,说明理由.
相切的圆?若能,请写出作法,画图并求出圆的半径;若不能,说明理由.
【答案】能够作出满足题设条件的圆
【解析】
能够作出满足题设条件的圆.
作法:1.过![]() 、
、![]() 两点任作一
两点任作一![]() .
.
2.作直线![]() 交直线
交直线![]() 于
于![]() .
.
3.过![]() 作
作![]() 的切线
的切线![]() ,
,![]() 为切点.
为切点.
4.以![]() 点为圆心,
点为圆心,![]() 为半径画弧交直线
为半径画弧交直线![]() 于
于![]() 、
、![]() 两点.
两点.
5.过![]() 、
、![]() 、
、![]() 三点或
三点或![]() 、
、![]() 、
、![]() 三点作
三点作![]() 或
或![]() .
.
因此,![]() ,
,![]() 均为所求作的圆.
均为所求作的圆.
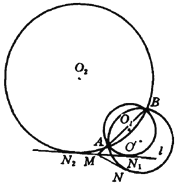
证明:![]() 是
是![]() 的切线,
的切线,![]() .
.
![]() ,
,![]() .
.
由圆的切割线定理的逆定理知,![]() 为
为![]() 的切线,即
的切线,即![]() 与
与![]() 相切.
相切.
又![]() 经过
经过![]() 、
、![]() 两点,因此,
两点,因此,![]() 是符合题设条件的圆.
是符合题设条件的圆.
同理,![]() 也是符合题设条件的圆.
也是符合题设条件的圆.
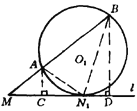
解法一:如图.过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,连结
,连结![]() 、
、![]() .则
.则
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
由切割线定理,得![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() .
.
![]() .
.
![]() .
.
又![]() ,
,
由正弦定理,得![]() ,故
,故![]() .
.
如图.连结![]() ,
,![]() .
.![]() ,
,
![]() ,
,
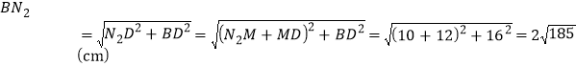 .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() ,
,![]() .
.
由正弦定理,得![]() ,故
,故![]() .
.
因此,所求圆的半径为![]() 或
或![]() .
.
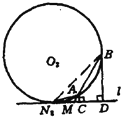
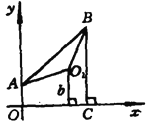
解法二:如图.以直线![]() 为
为![]() 轴,过
轴,过![]() 点垂直于
点垂直于![]() 的直线为
的直线为![]() 轴建立直角坐标系,
轴建立直角坐标系,![]() 于
于![]() .则
.则![]() ,有
,有![]() ,
,![]() .
.
设所求的圆的圆心![]() 的坐标为
的坐标为![]() ,则半径
,则半径![]() 应为
应为![]() .
.
![]() .
.![]() .
.
解之,得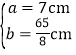 或
或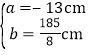 .
.
故所求圆的半径为![]() 或
或![]() .
.
注:本题也可先求出![]() ,
,![]() 的值,从而由
的值,从而由![]() 、
、![]() 、
、![]() 作圆.
作圆.


科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:![]() ,
,

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:某射手射击一次,击中目标的概率是0.9,他连续射击三次,且他每次射击是否击中目标之间没有影响,有下列结论:①他三次都击中目标的概率是![]() ;②他第三次击中目标的概率是
;②他第三次击中目标的概率是![]() ; ③他恰好2次击中目标的概率是
; ③他恰好2次击中目标的概率是![]() ;④他至少
;④他至少![]() 次击中目标的概率是
次击中目标的概率是![]() ;⑤他至多2次击中目标的概率是
;⑤他至多2次击中目标的概率是![]() .其中正确命题的序号是 ________(正确命题的序号全填上).
.其中正确命题的序号是 ________(正确命题的序号全填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:

设农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() =bx+a;
=bx+a;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注:![]() =
= =
= ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1998年,某地在抗洪抢险中接到预报,24小时后有一个超历史最高水位的洪峰到达,为保万无一失,指挥部决定在24小时内筑起一道堤坝作为第二防线.经计算,其工程量除动用现有军民连续奋战外,还需要20台大型翻斗车同时作业24小时.但是,除了第一辆车可以立即调入工作外,其余车辆需从各单位紧急抽调,每隔20分钟有一辆车到达投入作业,已知指挥部最多能组织到25辆车.问24小时内能否完成第二防线工程?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔![]() (单位:分钟)满足
(单位:分钟)满足![]() .经测算,地铁载客量与发车时间间隔
.经测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时地铁为满载状态,载客量为
时地铁为满载状态,载客量为![]() 人,当
人,当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为
的平方成正比,且发车时间间隔为![]() 分钟时的载客量为
分钟时的载客量为![]() 人,记地铁载客量为
人,记地铁载客量为![]() .
.
(1)求![]() 的表达式,并求当发车时间间隔为
的表达式,并求当发车时间间隔为![]() 分钟时,地铁的载客量;
分钟时,地铁的载客量;
(2)若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?每分钟的最大净收益为多少?
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?每分钟的最大净收益为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com