
【题目】已知椭圆![]() 过点
过点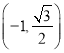 且离心率为
且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
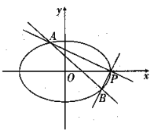
(2)如图所示,设椭圆![]() 的右顶点为
的右顶点为![]() ,
,![]() ,
,![]() 是椭圆上异于点
是椭圆上异于点![]() 的两点,直线
的两点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,试判断直线
,试判断直线![]() 是否经过一个定点?若是,则求出该定点的坐标;若不是,请说明理由.
是否经过一个定点?若是,则求出该定点的坐标;若不是,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() :
:![]() 的焦点
的焦点![]() ,且与拋物线
,且与拋物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)设点![]() 在笫一象限,过
在笫一象限,过![]() 作拋物线
作拋物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.

(Ⅰ)求这两个班学生成绩的中位数及x的值;
(Ⅱ)如果将这些成绩分为“优秀”(得分在175分 以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原,如图所示,平行四边形形状的纸片是由六个边长为![]() 的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球体积的最大值为______.
的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球体积的最大值为______.
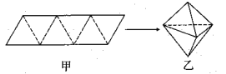
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物公司将A型病毒疫苗用100只小白鼠进行科研和临床试验,得到统计数据如表:
未感染病毒 | 感染病毒 | 总计 | |
未注射 | 10 | x | A |
注射 | 40 | y | B |
总计 | 50 | 50 | 100 |
现从所有试验的小白鼠中任取一只,取得注射疫苗小白鼠的概率为![]() .
.
(1)能否有99.9%的把握认为注射此型号疫苗有效?
(2)现从感染病毒的小白鼠中任取3只进行病理分析,记已注射疫苗的小白鼠只数为ξ,求ξ的分布列和数学期望.
附: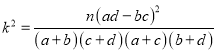
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点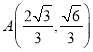 ,其左、右两个焦点分别为
,其左、右两个焦点分别为![]() ,
,![]() ,短轴的一个端点为
,短轴的一个端点为![]() ,且
,且![]() .
.
(1)求![]() 的平分线所在的直线方程;
的平分线所在的直线方程;
(2)设直线![]() :
:![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,
,![]() .且
.且![]() 为坐标原点,若
为坐标原点,若![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com