
【题目】设f(x)是定义在R上的可导函数,且满足f′(x)>f(x),对任意的正数a,下面不等式恒成立的是( )
A.f(a)<eaf(0)
B.f(a)>eaf(0)
C.![]()
D.![]()
【答案】B
【解析】解:∵f(x)是定义在R上的可导函数,
∴可以令f(x)= ![]() ,
,
∴f′(x)= ![]() =
= ![]() ,
,
∵f′(x)>f(x),ex>0,
∴f′(x)>0,
∴f(x)为增函数,
∵正数a>0,
∴f(a)>f(0),
∴ ![]() >
> ![]() =f(0),
=f(0),
∴f(a)>eaf(0),
故选B.
【考点精析】本题主要考查了基本求导法则和利用导数研究函数的单调性的相关知识点,需要掌握若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
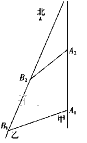
【题目】如图,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立坐标系.已知曲线C:ρsin2θ=2acosθ(a>0),过点P(﹣2,﹣4)的直线l的参数方程为 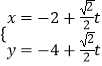 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(1)写出曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() x+
x+![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com