
【题目】如图,在平面直角坐标系xOy中,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,点P是椭圆E上一点,满足
的左,右焦点,点P是椭圆E上一点,满足![]() 轴,
轴,![]() .
.
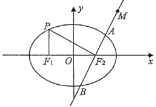
(1)求椭圆E的离心率;
(2)过点![]() 的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() ,
,![]() ,
,![]() ,建立
,建立![]() 的方程即可求解(2)斜率不存在时不符合题意,斜率存在时利用平行四边形的对角线互相平分,求出AB 中点,可得出Q坐标,利用点在椭圆上上求出斜率.
的方程即可求解(2)斜率不存在时不符合题意,斜率存在时利用平行四边形的对角线互相平分,求出AB 中点,可得出Q坐标,利用点在椭圆上上求出斜率.
(1)由![]() 轴,得
轴,得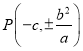 ,所以
,所以![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() ,得
,得![]() ,
,
解得![]() 或
或![]() (舍),所以
(舍),所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
椭圆E方程可化为![]() .
.
若直线l斜率不存在,直线![]() ,与椭圆E只有一个交点,不成立.
,与椭圆E只有一个交点,不成立.
(法一)设直线l方程为![]() ,
,![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
因为直线l过点![]() ,所以
,所以![]() ,
,
联立方程组![]() ,得
,得![]() .
.
![]() ,得
,得![]() .
.
由韦达定理,![]() ,
,![]() ,
,
得![]() ,
,![]() ,即点.
,即点.
因为平行四边形OAQB,所以点![]() ,
,
因为点Q在椭圆上,所以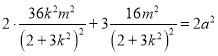 ,
,
化简得![]() .
.
由![]() ,得
,得![]() ,解得
,解得![]() .
.
(法二)设直线l的方程为![]() ,
,![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,得
,得![]() .
.
由韦达定理,![]() ,
,![]() ,
,
得![]() ,
,![]() ,即点
,即点![]() .
.
因为平行四边形OAQB,所以点![]() ,
,
因为点Q在椭圆上,所以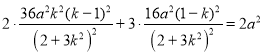 ,
,
化简得![]() ,解得
,解得![]() .
.


科目:高中数学 来源: 题型:
【题目】为了解一款电冰箱的使用时间和市民对这款电冰箱的购买意愿,研究人员对该款电冰箱进行了相应的抽样调查,得到数据的统计图表如下:
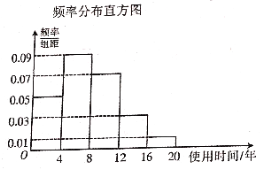
购买意愿市民年龄 | 不愿意购买该款电冰箱 | 愿意购买该款电冰箱 | 总计 |
40岁以上 | 600 | 800 | |
40岁以下 | 400 | ||
总计 | 800 |
(1)根据图中的数据,估计该款电冰箱使用时间的中位数;
(2)完善表中数据,并据此判断是否有![]() 的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
(3)用频率估计概率,若在该电冰箱的生产线上随机抽取3台,记其中使用时间不低于4年的电冰箱的台数为![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
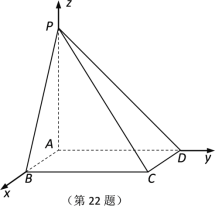
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5,该纸片上的等边三角形ABC的中心为O,点D,E,F为圆O上的点,![]() ,
,![]() ,
,![]() 分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起
分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起![]() ,
,![]() ,
,![]() ,使得D,E,F重合于P,得到三棱锥
,使得D,E,F重合于P,得到三棱锥![]() .
.

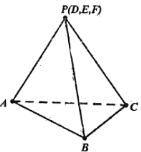
(1)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积;
的体积;
(2)当![]() 的边长变化时,三棱锥
的边长变化时,三棱锥![]() 的侧面和底面所成二面角为
的侧面和底面所成二面角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,当点E在B1D1(与B1,D1不重合)上运动时,总有:
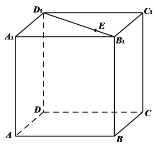
①AE∥BC1; ②平面AA1E⊥平面BB1D1D;
③AE∥平面BC1D; ④A1C⊥AE.
以上四个推断中正确的是( )
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4名运动员参加一次乒乓球比赛,每![]() 名运动员都赛
名运动员都赛![]() 场并决出胜负.设第
场并决出胜负.设第![]() 位运动员共胜
位运动员共胜![]() 场,负
场,负![]() 场
场![]() ,则错误的结论是( )
,则错误的结论是( )
A. ![]()
B. ![]()
C. ![]() 为定值,与各场比赛的结果无关
为定值,与各场比赛的结果无关
D. ![]() 为定值,与各场比赛结果无关
为定值,与各场比赛结果无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x∈R,x2+2x≥a,q:x2﹣4x+3≤0,r:(x﹣m)[x﹣(m+1)]≤0.
(1)若命题p的否定是假命题,求实数a的取值范围;
(2)若q是r的必要条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com