
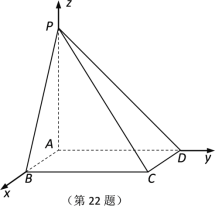
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
【答案】(1)![]() ;(2)M为AB的中点,N为PC的中点
;(2)M为AB的中点,N为PC的中点
【解析】
(1)由题意知,AB,AD,AP两两垂直.以![]() 为正交基底,建立空间直角坐标系
为正交基底,建立空间直角坐标系![]() ,求平面PCD的一个法向量为
,求平面PCD的一个法向量为![]() ,由空间向量的线面角公式求解即可;(2)设
,由空间向量的线面角公式求解即可;(2)设![]()
![]() ,利用
,利用![]() 平面PCD,所以
平面PCD,所以![]() ∥
∥![]() ,得到
,得到![]() 的方程,求解即可确定M,N的位置
的方程,求解即可确定M,N的位置
(1)由题意知,AB,AD,AP两两垂直.
以![]() 为正交基底,建立如图所示的空间
为正交基底,建立如图所示的空间
直角坐标系![]() ,则
,则![]()
从而![]()
设平面PCD的法向量![]()
则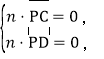 即
即![]()
不妨取![]() 则
则![]() .
.
所以平面PCD的一个法向量为![]() .
.
设直线PB与平面PCD所成角为![]() 所以
所以
即直线PB与平面PCD所成角的正弦值为![]() .
.
(2)设![]() 则
则![]()
设![]() 则
则![]() 而
而![]()
所以![]() .由(1)知,平面PCD的一个法向量为
.由(1)知,平面PCD的一个法向量为![]() ,因为
,因为![]() 平面PCD,所以
平面PCD,所以![]() ∥
∥![]() .
.
所以![]() 解得,
解得,![]() .
.
所以M为AB的中点,N为PC的中点.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)设函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,若函数
,若函数![]() 是
是![]() 上的单调增函数,求
上的单调增函数,求![]() 的值;
的值;
(3)是否存在一条直线与函数![]() 的图象相切于两个不同的点?并说明理由.
的图象相切于两个不同的点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
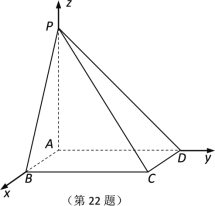
【题目】我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称之为堑堵;将底面为矩形且一侧棱垂直于底面的四棱锥称之为阳马;将四个面均为直角三角形的四面体称之为鳖臑[biē nào].某学校科学小组为了节约材料,拟依托校园内垂直的两面墙和地面搭建一个堑堵形的封闭的实验室![]() ,
,![]() 是边长为2的正方形.
是边长为2的正方形.


(1)若![]() 是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
(2)若![]() ,
,![]() 在
在![]() 上,证明:
上,证明:![]() ,并回答四面体
,并回答四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)当阳马![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
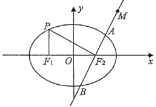
【题目】如图,在平面直角坐标系xOy中,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左,右焦点,点P是椭圆E上一点,满足
的左,右焦点,点P是椭圆E上一点,满足![]() 轴,
轴,![]() .
.
(1)求椭圆E的离心率;
(2)过点![]() 的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
的直线l与椭圆E交于两点A,B,若在椭圆B上存在点Q,使得四边形OAQB为平行四边形,求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
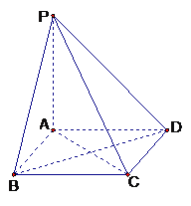
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛,其中3名来自A学校且1名为女棋手,另外4名来自B学校且2名为女棋手![]() 从这7名队员中随机选派4名队员参加第一阶段的比赛
从这7名队员中随机选派4名队员参加第一阶段的比赛
![]() 求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
求在参加第一阶段比赛的队员中,恰有1名女棋手的概率;
![]() Ⅱ
Ⅱ![]() 设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望
设X为选出的4名队员中A、B两校人数之差的绝对值,求随机变量X的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com