
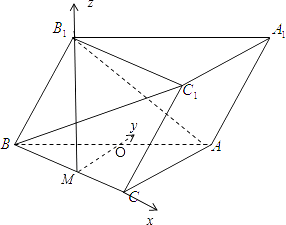
【题目】如图,斜三棱柱ABC﹣A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2. 
(1)求证:平面ACC1A1⊥平面B1C1CB;
(2)若二面角B﹣AB1﹣C1的余弦值为 ![]() ,求斜三棱柱ABC﹣A1B1C1的侧棱AA1的长度.
,求斜三棱柱ABC﹣A1B1C1的侧棱AA1的长度.
【答案】
(1)解:取BC中点M,连接B1M,则B1M⊥面ABC,
∴面BB1C1C⊥面ABC,
∵BC=面BB1C1C∩面ABC,AC⊥BC,
∴AC⊥面BB1C1C,
∵AC面ACC1A1∴面ACC1A1⊥面BCC1B1
(2)解:取BC的中点为M,AB的中点M,连接OM,MB1,
以MC为x轴,MO为y轴,MB1为z轴,建立空间直角坐标系.AC=BC=2,AB=2 ![]() ,设B1M=t,则A(1,2,0),B(﹣1,0,0),C(1,0,0),B1(0,0,t),C1(2,0,t),
,设B1M=t,则A(1,2,0),B(﹣1,0,0),C(1,0,0),B1(0,0,t),C1(2,0,t),
则 ![]() =(﹣1,﹣2,t),
=(﹣1,﹣2,t), ![]() =(﹣2,﹣2,0),
=(﹣2,﹣2,0), ![]() =(2,0,0),
=(2,0,0),
设平面AB1C1法向量 ![]() ,
,
∴ 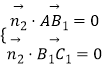 ,即
,即 ![]() ,取
,取 ![]() =
= ![]() .
.
同理可得面AB1B法向量 ![]() =(1,﹣1,﹣
=(1,﹣1,﹣ ![]() ).
).
∵ ![]() =
= ![]() =
= 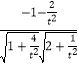 ,
,
t4+29t2﹣96=0,
∴t= ![]() ,
,
∴BB1=2.
【解析】(1)利用线面垂直的性质定理证明面面垂直(2)建立空间直角坐标系,写出对应点的坐标,利用余弦值求得边长.


科目:高中数学 来源: 题型:
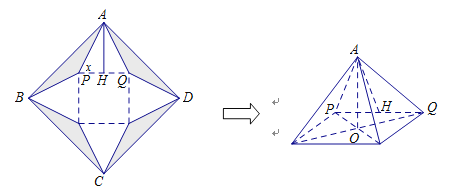
【题目】如图:设一正方形纸片ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中![]() ,O为正四棱锥底面中心.
,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴负半轴相交于点
轴负半轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() .
.
(1)若过点 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若在以![]() 为圆心半径为
为圆心半径为![]() 的圆上存在点
的圆上存在点![]() ,使得
,使得![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围;
的取值范围;
(3)设![]() 是圆
是圆![]() 上的两个动点,点
上的两个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,如果直线
,如果直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 和
和![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
(1)求椭圆C的方程;
(2)如图,直线l:y=kx+m与椭圆C相交于P,Q两点,若在椭圆C上存在点R,使OPRQ为平行四边形,求m的取值范围. 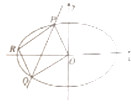
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同轨班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)
(1)经过多次测试后,小明正确解答一道数学应用题所用的时
间在5—7分钟,小刚正确解得一道数学应用题所用的时间在6—8
分钟,现小明.小刚同时独立解答同一道数学应用题,求小刚比
小明先正确解答完的概率;
(2)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们的答题情况进行全程研究,记A.B两人中被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国大学生机器人大赛是由共青团中央,全国学联,深圳市人民政府联合主办的赛事,是中国最具影响力的机器人项目,是全球独创的机器人竞技平台.全国大学生机器人大赛比拼的是参赛选手们的能力,坚持和态度,展现的是个人实力以及整个团队的力量.2015赛季共吸引全国240余支机器人战队踊跃报名,这些参赛战队来自全国六大赛区,150余所高等院校,其中不乏北京大学,清华大学,上海交大,中国科大,西安交大等众多国内顶尖高校,经过严格筛选,最终由111支机器人战队参与到2015年全国大学生机器人大赛的激烈角逐之中,某大学共有“机器人”兴趣团队1000个,大一、大二、大三、大四分别有100,200,300,400个,为挑选优秀团队,现用分层抽样的方法,从以上团队中抽取20个团队.
(1)应从大三抽取多少个团队?
(2)将20个团队分为甲、乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲、乙两组的分数如下:
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
从甲、乙两组中选一组强化训练,备战机器人大赛.从统计学数据看,若选择甲组,理由是什么?若选择乙组,理由是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一直一艘船由![]() 岛以
岛以![]() 海里/小时的速度往北偏东
海里/小时的速度往北偏东![]() 的
的![]() 岛形式,计划到达
岛形式,计划到达![]() 岛后停留
岛后停留![]() 分钟后继续以相同的速度驶往
分钟后继续以相同的速度驶往![]() 岛.
岛.![]() 岛在
岛在![]() 岛的北偏西
岛的北偏西![]() 的方向上,
的方向上,![]() 岛也也在
岛也也在![]() 岛的北偏西
岛的北偏西![]() 的方向上.上午
的方向上.上午![]() 时整,该船从
时整,该船从![]() 岛出发.上午
岛出发.上午![]() 时
时![]() 分,该船到达
分,该船到达![]() 处,此时测得
处,此时测得![]() 岛在北偏西
岛在北偏西![]() 的方向上.如果一切正常,此船何时能到达
的方向上.如果一切正常,此船何时能到达![]() 岛?(精确到
岛?(精确到![]() 分钟)
分钟)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com