
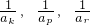 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由;
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由; .
.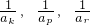 成等差数列,则
成等差数列,则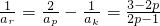 ,
,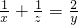 ,所以
,所以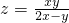 ,(7分)
,(7分)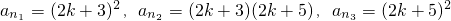 ,其中k∈N*,
,其中k∈N*,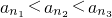 ,
,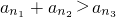 ,所以它们能组成三角形.
,所以它们能组成三角形.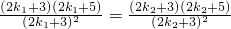 ,
,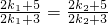 ,所以k1=k2,这与条件k1≠k2相矛盾,
,所以k1=k2,这与条件k1≠k2相矛盾,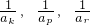 成等差数列,则
成等差数列,则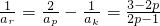 ,再由题设条件分类讨论知当k=1时,不存在p,r;当k≥2时,存在p=2k-1,r=4k2-5k+2满足题设.
,再由题设条件分类讨论知当k=1时,不存在p,r;当k≥2时,存在p=2k-1,r=4k2-5k+2满足题设.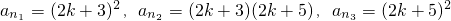 ,其中k∈N*,它们依次为数列an中的第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13项,显然它们成等比数列,且
,其中k∈N*,它们依次为数列an中的第2k2+6k+5项,第2k2+8k+8项,第2k2+10k+13项,显然它们成等比数列,且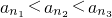 ,所以它们能组成三角形.由k∈N*的任意性,这样的三角形有无穷多个.再用反证法证明其中任意两个三角形A1B1C1和A2B2C2不相似.
,所以它们能组成三角形.由k∈N*的任意性,这样的三角形有无穷多个.再用反证法证明其中任意两个三角形A1B1C1和A2B2C2不相似.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| n |
| an |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| ak |
| 1 |
| ap |
| 1 |
| ar |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
| 2 |
| n |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com