已知{an}是单调递增的等差数列,首项a1=3,前n项和为Sn,数列{bn}是等比数列,首项b1=1,且a2b2=12,S3+b2=20.
(Ⅰ)求{an}和{bn}的通项公式.
(Ⅱ)令Cn=Sncos(anπ)(n∈N+),求{cn}的前n项和Tn.
【答案】
分析:(Ⅰ)根据题意,设{a
n}的公差为d,{b
n}的公比为q,由已知条件a
2b
2=12,S
3+b
2=20,可得关于d、q的方程组,求解可得d、q的值,结合等比等差数列的通项公式,可得答案;
(Ⅱ)由(Ⅰ)的结论,可得C
n的表达式,即
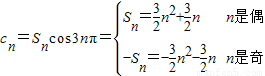
,分n为奇数与偶数两种情况讨论,计算可得答案.
解答:解:(Ⅰ)设{a
n}的公差为d,{b
n}的公比为q,
则a
2b
2=(3+d)q=12,①
S
3+b
2=3a
2+b
2=3(3+d)+q=9+3d+q=20,即3d+q=11,
变形可得q=11-3d,②
代入①可得:(3+d)(11-d)=33+2d-3d
2=12,
3d
2-2d-21=0,
(3d+7)(d-3)=0,
又由{a
n}是单调递增的等差数列,有d>0.
则d=3,
q=11-3d=2,
a
n=3+(n-1)×3=3n,b
n=2
n-1…(6分)
(Ⅱ)
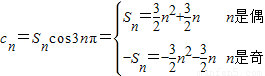
…(9分)
当n是偶数,T
n=c
1+c
2+c
3+…+c
n=-S
1+S
2-S
3+S
4-…-S
n-1+S
n=
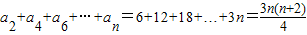
…(10分)
当n是奇数,
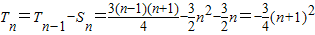
综上可得
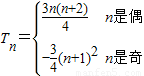
…(13分)
点评:本题综合考查等比、等差数列,涉及数列的求和;解(Ⅱ)题的关键在于分析发现T
n与C
n的关系,转化来求出答案,注意要分n为奇数与偶数2种情况进行讨论.

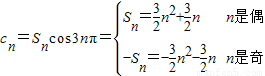 ,分n为奇数与偶数两种情况讨论,计算可得答案.
,分n为奇数与偶数两种情况讨论,计算可得答案.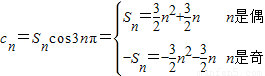 …(9分)
…(9分)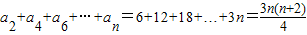 …(10分)
…(10分)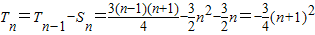
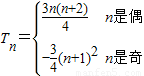 …(13分)
…(13分)
