练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某射击运动员在比赛前进行三周的封闭训练，教练员将其每天成绩的均值数据整理，并绘成条形图如下，

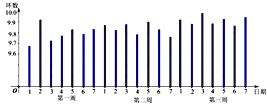
    根据该图，下列说法错误的是：（ ）

    A.第三周平均成绩最好B.第一周平均成绩比第二平均成绩好

    C.第一周成绩波动较大D.第三周成绩比较稳定

    【答案】B

    【解析】

    根据条形图即可比较平均值、波动情况.

    对于A，由条形图可知，第三周的环数普遍高于前两周的环数，

    故第三周的平均成绩最好，故A正确；

    对于B，由图可知，第二周的环数稍高于第一周的环数，

    故第二周的平均成绩比第一周的平均成绩好，故B错误；

    对于C，由图可知，第一周每天的环数差距比第二周、第三周大，

    故第一周成绩波动较大，故C正确；

    对于D，由图可知，第三周每天的环数差距较小，

    故第三周的波动较小，成绩比较稳定，故D正确

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数在处的切线方程为.

    (1)求函数的解析式；

    (2)若关于的方程恰有两个不同的实根,求实数的值；

    (3)数列满足.

    证明：①；

    ②.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某周末，郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”，成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客（这些游客只在两个主题公园中二选一）进行了问卷调查.调查结果显示，在被调查的50位成年人中，只有10人选择“西游传说”，而选择“西游传说”的未成年人有20人.

    （1）根据题意，请将下面的列联表填写完整；

    选择“西游传说”

    选择“千古蝶恋”

    总计

    成年人

    未成年人

    总计

    （2）根据列联表的数据，判断是否有的把握认为选择哪个主题公园与年龄有关.

    附参考公式与表：（）.

    0.100

    0.050

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R的奇函数满足，且时， ，下面四种说法①；②函数在［-6，-2］上是增函数；③函数关于直线对称；④若，则关于的方程在［-8，8］上所有根之和为-8，其中正确的序号__________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学将100名高一新生分成水平相同的甲，乙两个“平行班”，每班50人.陈老师采用A，B两种不同的教学方式分别在甲，乙两个班级进行教改实验.为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下，计成绩不低于90分者为“成绩优秀”.

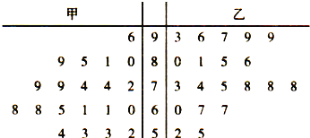
    （1）从乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率.

    （2）由以上统计数据填写下面2×2列联表，并判断是否有90%的把握认为“成绩优秀”与教学方式有关.

    甲班（A方式）

    乙班（B方式）

    总计

    成绩优秀

    成绩不优秀

    总计

    附：临界值表

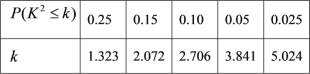
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年春季，某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车，现有两款车型，根据以往这两种出租车车型的数据，得到两款出租车车型使用寿命频数表如下：

    使用寿命年数

    5年

    6年

    7年

    8年

    总计

    型出租车(辆)

    10

    20

    45

    25

    100

    型出租车(辆)

    15

    35

    40

    10

    100

    （1）填写下表，并判断是否有的把握认为出租车的使用寿命年数与汽车车型有关？

    使用寿命不高于年

    使用寿命不低于年

    总计

    型

    型

    总计

    （2）司机师傅小李准备在一辆开了年的型车和一辆开了年的型车中选择，为了尽最大可能实现年内（含年）不换车，试通过计算说明，他应如何选择.

    附：，.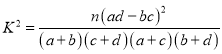

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据，整理如下：

    甲公司员工：410，390，330，360，320，400，330，340，370，350

    乙公司员工：360，420，370，360，420，340，440，370，360，420

    每名快递员完成一件货物投递可获得的劳务费情况如下：甲公司规定每件0.65元，乙公司规定每天350件以内(含350件)的部分每件0.6元，超出350件的部分每件0.9元.

    （1）根据题中数据写出甲公司员工在这10天投递的快件个数的平均数和众数；

    （2）为了解乙公司员工每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为 (单位：元)，求的分布列和数学期望；

    （3）根据题中数据估算两公司被抽取员工在该月所得的劳务费.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的参数方程为（为参数）.以直角坐标系的原点为极点，轴的正半轴为极轴建立坐标系，曲线的极坐标方程为.

    （1）求的普通方程和的直角坐标方程；

    （2）若过点的直线与交于，两点，与交于，两点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年3月份，上海出台了《关于建立完善本市生活垃圾全程分类体系的实施方案》，4月份又出台了《上海市生活垃圾全程分类体系建设行动计划（2018-2020年）》，提出到2020年底，基本实现单位生活垃圾强制分类全覆盖，居民区普遍推行生活垃圾分类制度．为加强社区居民的垃圾分类意识，推动社区垃圾分类正确投放，某社区在健身广场举办了“垃圾分类，从我做起”生活垃圾分类大型宣传活动，号召社区居民用实际行动为建设绿色家园贡献一份力量，为此需要征集一部分垃圾分类志愿者．

    （1）为调查社区居民喜欢担任垃圾分类志愿者是否与性别有关，现随机选取了一部分社区居民进行调查，其中被调查的男性居民和女性居民人数相同，男性居民中不喜欢担任垃圾分类志愿者占男性居民的，女性居民中不喜欢担任垃圾分类志愿者占女性居民的，若研究得到在犯错误概率不超过0.010的前提下，认为居民喜欢担任垃圾分类志愿者与性别有关，则被调查的女性居民至少多少人？

    附，，

    0.100

    0.050

    0.010

    0.005

    0.001

    2.706

    3.841

    6.635

    7.879

    10.828

    （2）某垃圾站的日垃圾分拣量（千克）与垃圾分类志愿者人数（人）满足回归直线方程，数据统计如下：

    志愿者人数（人）

    2

    3

    4

    		5

    6

    日垃圾分拣量（千克）

    25

    30

    40

    45

    已知，，，根据所给数据求和回归直线方程，附：，．

    （3）用（2）中所求的线性回归方程得到与对应的日垃圾分拣量的估计值．当分拣数据与估计值满足时，则将分拣数据称为一个“正常数据”．现从5个分拣数据中任取3个，记表示取得“正常数据”的个数，求的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案