
如图(1),从边长为2a的正方形铁片的四个角各截一个边长为x的正方形,然后折成一个无盖的长方体盒子,如图(2),要求长方体的高度x与底面正方形边长的比不超过正常数t.
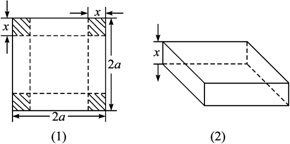
(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
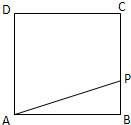 如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,
如图,动点P从边长为1的正方形ABCD的顶点A开始,顺次经B、C、D绕边界一周,当x表示点P的行程,y表示PA之长时,查看答案和解析>>
科目:高中数学 来源: 题型:
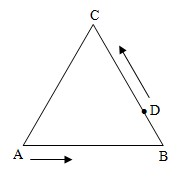 例2:如图:△ABC是边长为3厘米的正三角形,D是BC边上靠近点B的三等分点,甲、乙两个质点分别从点A、D同时出发,都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动,经过时间t(0≤t≤3)秒后,两质点的距离为S(t).
例2:如图:△ABC是边长为3厘米的正三角形,D是BC边上靠近点B的三等分点,甲、乙两个质点分别从点A、D同时出发,都以1厘米/秒的速度按图示方向沿三角形的边作匀速运动,经过时间t(0≤t≤3)秒后,两质点的距离为S(t).查看答案和解析>>
科目:高中数学 来源: 题型:

图1-3-14
A.258 B.234 C.222 D.210
查看答案和解析>>
科目:高中数学 来源:2008-2009学年上海市奉贤区曙光中学高三第二轮复习专题试卷(函数中的应用题)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com