
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)当
的减区间;(2)当![]() 时,不等式
时,不等式![]() 在
在![]() 时恒成立,等价于
时恒成立,等价于![]() 在(1,+∞)上恒成立,令
在(1,+∞)上恒成立,令![]() ,先证明当
,先证明当![]() 时,不合题意,再分两种情况讨论即可筛选出符合题意的实数
时,不合题意,再分两种情况讨论即可筛选出符合题意的实数![]() 的取值范围.
的取值范围.
(1)由题意,知![]() ,
,
∵当a<0,x>0时,有![]() .
.
∴x>1时,![]() ;当0<x<1时,
;当0<x<1时,![]() .
.
∴函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)由题意,当a=1时,不等式![]() 在x∈(1,+∞)时恒成立.
在x∈(1,+∞)时恒成立.
整理,得![]() 在(1,+∞)上恒成立.
在(1,+∞)上恒成立.
令![]() .
.
易知,当b≤0时,![]() ,不合题意.
,不合题意.
∴b>0
又![]() ,
,![]() .
.
①当b≥![]() 时,
时,![]() .又
.又![]() 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.
∴![]() 在[1,+∞)上恒成立,则h(x)在[1,+∞)上单调递减.
在[1,+∞)上恒成立,则h(x)在[1,+∞)上单调递减.
所以![]() ,符合题意;
,符合题意;
②![]() 时,
时,![]() ,
,![]() ,
,
又![]() 在[1,+∞)上单调递减,
在[1,+∞)上单调递减,
∴存在唯一x0∈(1,+∞),使得![]() .
.
∴当h(x)在(1,x0)上单调递增,在(x0,+∞)上单调递减.
又h(x)在x=1处连续,h(1)=0,∴h(x)>0在(1,x0)上恒成立,不合题意.
综上所述,实数b的取值范围为[![]() ,+∞ ).
,+∞ ).


科目:高中数学 来源: 题型:
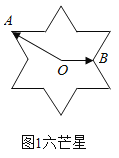
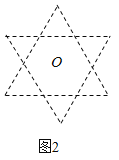
【题目】如图,“六芒星”是由两个全等正三角形组成,中心重合于点![]() 且三组对边分别平行,点
且三组对边分别平行,点![]() 是“六芒星”(如图)的两个顶点,动点
是“六芒星”(如图)的两个顶点,动点![]() 在“六芒星”上(内部以及边界),若
在“六芒星”上(内部以及边界),若![]() ,则
,则![]() 的取值可能是( )
的取值可能是( )
A.![]() B.1C.5D.9
B.1C.5D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数.f(t),随时刻t(时)变化的规律满足表达式![]() ,其中a为空气治理调节参数,且a∈(0,1).
,其中a为空气治理调节参数,且a∈(0,1).
(1)令![]() ,求x的取值范围;
,求x的取值范围;
(2)若规定每天中f(t)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: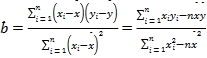 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com