
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用代入法消去参数方程中的参数可求直线![]() 的普通方程,极坐标方程展开后,两边同乘以
的普通方程,极坐标方程展开后,两边同乘以![]() ,利用
,利用![]() ,即可得曲线
,即可得曲线![]() 的直角坐标方程;(2)直线
的直角坐标方程;(2)直线![]() 的参数方程代入圆
的参数方程代入圆![]() 的直角坐标方程,利用韦达定理、直线参数方程的几何意义即可得结果.
的直角坐标方程,利用韦达定理、直线参数方程的几何意义即可得结果.
(1)将直线l的参数方程消去参数t并化简,得
直线l的普通方程为![]() .
.
将曲线C的极坐标方程化为![]() .
.
即![]() .∴x2+y2=2y+2x.
.∴x2+y2=2y+2x.
故曲线C的直角坐标方程为![]() .
.
(2)将直线l的参数方程代入![]() 中,得
中,得
![]() .
.
化简,得![]() .
.
∵Δ>0,∴此方程的两根为直线l与曲线C的交点A,B对应的参数t1,t2.
由根与系数的关系,得![]() ,
,![]() ,即t1,t2同正.
,即t1,t2同正.
由直线方程参数的几何意义知,
![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
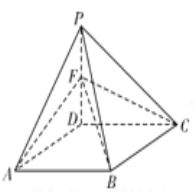
(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某个餐厅打算从上表的6种等级的中国小龙虾中随机选2种进行促销,记被选中的2种等级代码数值在60以下(不含60)的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:对一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: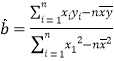 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位正![]() 内任取一点P,以PA、PB、PC为边生成
内任取一点P,以PA、PB、PC为边生成![]() .
.
(1)当![]() 分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
(2)证明:当![]() 的周长取最小值时,面积取最大值.
的周长取最小值时,面积取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆
,点P在直线l上,过点P作圆![]() 的切线PA,PB,切点为A,B.
的切线PA,PB,切点为A,B.
(1)若![]() ,求点P的坐标;
,求点P的坐标;
(2)求证:经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,并求该定点的坐标.
的某个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①由五个面围成的多面体只能是三棱柱;
②由若干个平面多边形所围成的几何体是多面体;
③仅有一组对面平行的五面体是棱台;
④有一面是多边形,其余各面是三角形的几何体是棱锥.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com