
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
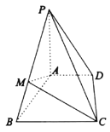
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用相似三角形证明出
,利用相似三角形证明出![]() ,可证明出四边形
,可证明出四边形![]() 是平行四边形,可得出
是平行四边形,可得出![]() ,再利用直线与平面平行的判定定理可证明出
,再利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)证明出![]() 平面
平面![]() ,可得出点
,可得出点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,然后作
的距离,然后作![]() 于
于![]() ,证明出
,证明出![]() 平面
平面![]() ,计算出
,计算出![]() ,即可得出点
,即可得出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)由题意,侧面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
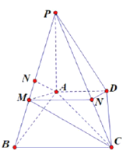
因为![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)由题设![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因此点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
作![]() 于
于![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 的长度就是点
的长度就是点![]() 到平面
到平面![]() 的距离.
的距离.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
则![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,
,
即点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知平面内一个动点M到定点F(3,0)的距离和它到定直线l:x=6的距离之比是常数![]() .
.
(1)求动点M的轨迹T的方程;
(2)若直线l:x+y-3=0与轨迹T交于A,B两点,且线段AB的垂直平分线与T交于C,D两点,试问A,B,C,D是否在同一个圆上?若是,求出该圆的方程;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 是曲线
是曲线![]() :
:![]() 上的一个动点,曲线
上的一个动点,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 是坐标原点,①
是坐标原点,①![]() ;②
;②![]() 的面积为定值;③曲线
的面积为定值;③曲线![]() 上存在两点
上存在两点![]() ,
,![]() 使得
使得![]() 是等边三角形;④曲线
是等边三角形;④曲线![]() 上存在两点
上存在两点![]() ,
,![]() 使得
使得![]() 是等腰直角三角形,其中真命题的个数是( )
是等腰直角三角形,其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点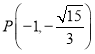 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,使得
两点,使得![]() ?若存在,求出直线的方程;若不存在,说明理由.
?若存在,求出直线的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推,若该数列前
,依此类推,若该数列前![]() 项和
项和![]() 满足:①
满足:①![]() ②
②![]() 是2的整数次幂,则满足条件的最小的
是2的整数次幂,则满足条件的最小的![]() 为
为
A. 21B. 91C. 95D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的一个顶点与抛物线
的一个顶点与抛物线![]() 的焦点重合,
的焦点重合,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,其离心率
的左、右焦点,其离心率![]() 椭圆
椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com