
ЁОЬтФПЁПЮЊбаОПЛМЗЮАЉгыЪЧЗёЮќбЬгаЙиЃЌзіСЫвЛДЮЯрЙиЕїВщЃЌЦфжаВПЗжЪ§ОнЖЊЪЇЃЌЕЋПЩвдШЗЖЈЕФЪЧВЛЮќбЬШЫЪ§гыЮќбЬШЫЪ§ЯрЭЌЃЌЮќбЬЛМЗЮАЉШЫЪ§еМЮќбЬзмШЫЪ§ЕФ![]() ЃЛВЛЮќбЬЕФШЫЪ§жаЃЌЛМЗЮАЉгыВЛЛМЗЮАЉЕФБШЮЊ
ЃЛВЛЮќбЬЕФШЫЪ§жаЃЌЛМЗЮАЉгыВЛЛМЗЮАЉЕФБШЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєЮќбЬВЛЛМЗЮАЉЕФга![]() ШЫЃЌЯжДгЛМЗЮАЉЕФШЫжагУЗжВуГщбљЕФЗНЗЈГщШЁ
ШЫЃЌЯжДгЛМЗЮАЉЕФШЫжагУЗжВуГщбљЕФЗНЗЈГщШЁ![]() ШЫЃЌдйДгет
ШЫЃЌдйДгет![]() ШЫжаЫцЛњГщШЁ
ШЫжаЫцЛњГщШЁ![]() ШЫНјааЕїВщЃЌЧѓетСНШЫЖМЪЧЮќбЬЛМЗЮАЉЕФИХТЪЃЛ
ШЫНјааЕїВщЃЌЧѓетСНШЫЖМЪЧЮќбЬЛМЗЮАЉЕФИХТЪЃЛ
ЃЈ2ЃЉШєбаОПЕУЕНдкЗИДэЮѓИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТЃЌШЯЮЊЛМЗЮАЉгыЮќбЬгаЙиЃЌдђЮќбЬЕФШЫЪ§жСЩйгаЖрЩйЃП
ЕФЧАЬсЯТЃЌШЯЮЊЛМЗЮАЉгыЮќбЬгаЙиЃЌдђЮќбЬЕФШЫЪ§жСЩйгаЖрЩйЃП
ИНЃК 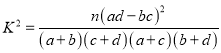 ЃЌЦфжа
ЃЌЦфжа![]() ЃЎ
ЃЎ
|
|
|
|
|
|
|
|
|
|
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЮќбЬШЫЪ§жСЩйЮЊ
ЃЛЃЈ2ЃЉЮќбЬШЫЪ§жСЩйЮЊ![]() ШЫЃЎ
ШЫЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіЮќбЬЕФШЫга![]() ШЫЃЌАДБШР§ПЩЕУЦфжаЗЮАЉЕФга16ШЫЃЌВЛЛМЗЮАЉЕФга4ШЫЃЌАДЗжВуГщбљЕФЖЈвхПЩЕУГщШЁЕФ5ШЫжаЃЌ4ШЫЛМВЁЃЌ1ШЫВЛЛМВЁЃЌРћгУСаОйЗЈПЩЕУГщШЁЗНЪНЙВга10жжЃЌЖМЛМВЁЕФ6жжЃЌгЩИХТЪМЦЫуЙЋЪНПЩЕУНсЙћЃЛЃЈ2ЃЉЩшЮќбЬШЫЪ§ЮЊ
ШЫЃЌАДБШР§ПЩЕУЦфжаЗЮАЉЕФга16ШЫЃЌВЛЛМЗЮАЉЕФга4ШЫЃЌАДЗжВуГщбљЕФЖЈвхПЩЕУГщШЁЕФ5ШЫжаЃЌ4ШЫЛМВЁЃЌ1ШЫВЛЛМВЁЃЌРћгУСаОйЗЈПЩЕУГщШЁЗНЪНЙВга10жжЃЌЖМЛМВЁЕФ6жжЃЌгЩИХТЪМЦЫуЙЋЪНПЩЕУНсЙћЃЛЃЈ2ЃЉЩшЮќбЬШЫЪ§ЮЊ![]() ЃЌСаГі
ЃЌСаГі![]() СаСЊБэЃЌгЩБэМЦЫуГі
СаСЊБэЃЌгЩБэМЦЫуГі![]() ЃЌИљОнБэЕУ
ЃЌИљОнБэЕУ![]() ЃЌНтГі
ЃЌНтГі![]() МДПЩЕУзюКѓНсЙћ.
МДПЩЕУзюКѓНсЙћ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшЮќбЬШЫЪ§ЮЊ![]() ЃЌвРЬтвтга
ЃЌвРЬтвтга![]() ЃЌЫљвдЮќбЬЕФШЫга
ЃЌЫљвдЮќбЬЕФШЫга![]() ШЫЃЌЙЪгаЮќбЬЛМЗЮАЉЕФга16ШЫЃЌВЛЛМЗЮАЉЕФга4ШЫЃЎгУЗжВуГщбљЕФЗНЗЈГщШЁ5ШЫЃЌдђгІГщШЁЮќбЬЛМЗЮАЉЕФ4ШЫЃЌМЧЮЊ
ШЫЃЌЙЪгаЮќбЬЛМЗЮАЉЕФга16ШЫЃЌВЛЛМЗЮАЉЕФга4ШЫЃЎгУЗжВуГщбљЕФЗНЗЈГщШЁ5ШЫЃЌдђгІГщШЁЮќбЬЛМЗЮАЉЕФ4ШЫЃЌМЧЮЊ![]() ЃЎВЛЮќбЬЛМЗЮАЉЕФ1ШЫЃЌМЧЮЊAЃЎДг5ШЫжаЫцЛњГщШЁ2ШЫЃЌЫљгаПЩФмЕФНсЙћга
ЃЎВЛЮќбЬЛМЗЮАЉЕФ1ШЫЃЌМЧЮЊAЃЎДг5ШЫжаЫцЛњГщШЁ2ШЫЃЌЫљгаПЩФмЕФНсЙћга![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЙВ
ЃЌЙВ![]() жжЃЌдђетСНШЫЖМЪЧЮќбЬЛМЗЮАЉЕФЧщаЮЙВга
жжЃЌдђетСНШЫЖМЪЧЮќбЬЛМЗЮАЉЕФЧщаЮЙВга![]() жжЃЌЁр
жжЃЌЁр![]() ЃЌМДетСНШЫЖМЪЧЮќбЬЛМЗЮАЉЕФИХТЪЮЊ
ЃЌМДетСНШЫЖМЪЧЮќбЬЛМЗЮАЉЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЩшЮќбЬШЫЪ§ЮЊ![]() ЃЌгЩЬтвтПЩЕУСаСЊБэШчЯТЃК
ЃЌгЩЬтвтПЩЕУСаСЊБэШчЯТЃК
ЛМЗЮАЉ | ВЛЛМЗЮАЉ | КЯМЦ | |
ЮќбЬ |
|
|
|
ВЛЮќбЬ |
|
|
|
змМЦ |
|
|
|
гЩБэЕУЃЌ  ЃЌгЩЬтвт
ЃЌгЩЬтвт![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёп![]() ЮЊећЪ§ЃЌЁр
ЮЊећЪ§ЃЌЁр![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() ЃЎдђ
ЃЎдђ![]() ЃЌМДЮќбЬШЫЪ§жСЩйЮЊ
ЃЌМДЮќбЬШЫЪ§жСЩйЮЊ![]() ШЫЃЎ
ШЫЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГШЫЩЯЮч7ЪБЃЌГЫФІЭаЭЇвддШЫйvkm/hЃЈ8ЁмvЁм40ЃЉДгAИлГіЗЂЕНОр100kmЕФBИлШЅЃЌШЛКѓГЫЦћГЕвддШЫйwkm/hЃЈ30ЁмwЁм100ЃЉздBИлЯђОр300kmЕФCЪаЪЛШЅЃЎгІИУдкЭЌвЛЬьЯТЮч4жС9ЕуЕНДяCЪаЃЎ ЩшГЫзјЦћГЕЁЂФІЭаЭЇШЅФПЕФЕиЫљашвЊЕФЪБМфЗжБ№ЪЧxhЃЌyhЃЎ
ЃЈ1ЃЉзїЭМБэЪОТњзуЩЯЪіЬѕМўЕФxЃЌyЗЖЮЇЃЛ
ЃЈ2ЃЉШчЙћвбжЊЫљашЕФОЗбp=100+3ЃЈ5ЉxЃЉ+2ЃЈ8ЉyЃЉЃЈдЊЃЉЃЌФЧУДvЃЌwЗжБ№ЪЧЖрЩйЪБpзюаЁЃПДЫЪБашЛЈЗбЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉТњзуfЃЈx+yЃЉ=fЃЈxЃЉfЃЈyЃЉЃЌЧвfЃЈ1ЃЉ= ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБnЁЪN*ЪБЃЌЧѓfЃЈnЃЉЕФБэДяЪНЃЛ
ЃЈ2ЃЉЩшan=nfЃЈnЃЉЃЌnЁЪN* ЃЌ ЧѓжЄa1+a2+a3+Ё+anЃМ2ЃЛ
ЃЈ3ЃЉЩшbn=ЃЈ9ЉnЃЉ ![]() ЃЌnЁЪN* ЃЌ SnЮЊbnЕФЧАnЯюКЭЃЌЕБSnзюДѓЪБЃЌЧѓnЕФжЕЃЎ
ЃЌnЁЪN* ЃЌ SnЮЊbnЕФЧАnЯюКЭЃЌЕБSnзюДѓЪБЃЌЧѓnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=lnЃЈ1+|x|ЃЉЉ ![]() ЃЌдђЪЙЕУfЃЈxЃЉЃОfЃЈ2xЉ1ЃЉГЩСЂЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЃЌдђЪЙЕУfЃЈxЃЉЃОfЃЈ2xЉ1ЃЉГЩСЂЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
A.ЃЈЉЁоЃЌ ![]() ЃЉЁШЃЈ1ЃЌ+ЁоЃЉ
ЃЉЁШЃЈ1ЃЌ+ЁоЃЉ
B.ЃЈ ![]() ЃЌ1ЃЉ
ЃЌ1ЃЉ
C.ЃЈ ![]() ЃЉ
ЃЉ
D.ЃЈЉЁоЃЌЉ ![]() ЃЌЃЉ
ЃЌЃЉ ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧдВOЕФжБОЖЃЌPAЁЭдВOЫљдкЕФЦНУцЃЌCЪЧдВOЩЯЕФЕуЃЎ 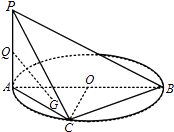
ЃЈ1ЃЉЧѓжЄЃКBCЁЭЦНУцPACЃЛ
ЃЈ2ЃЉШєQЮЊPAЕФжаЕуЃЌGЮЊЁїAOCЕФжиаФЃЌЧѓжЄЃКQGЁЮЦНУцPBCЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() ЕФзюжЕЃЎ
ЕФзюжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§fЃЈxЃЉ=cosЃЈІиx+ІеЃЉЃЈІиЃО0ЃЌ|Іе|ЃМ ![]() ЃЉЕФЭМЯѓЩЯЕФУПвЛЕуЕФзнзјБъВЛБфЃЌКсзјБъЫѕЖЬЮЊдРДЕФвЛАыЃЌдйНЋЭМЯѓЯђгвЦНвЦ
ЃЉЕФЭМЯѓЩЯЕФУПвЛЕуЕФзнзјБъВЛБфЃЌКсзјБъЫѕЖЬЮЊдРДЕФвЛАыЃЌдйНЋЭМЯѓЯђгвЦНвЦ ![]() ИіЕЅЮЛГЄЖШЕУЕНКЏЪ§y=sinxЕФЭМЯѓЃЎ
ИіЕЅЮЛГЄЖШЕУЕНКЏЪ§y=sinxЕФЭМЯѓЃЎ
ЃЈ1ЃЉжБНгаДГіfЃЈxЃЉЕФБэДяЪНЃЌВЂЧѓГіfЃЈxЃЉдк[0ЃЌІа]ЩЯЕФжЕгђЃЛ
ЃЈ2ЃЉЧѓГіfЃЈxЃЉдк[0ЃЌІа]ЩЯЕФЕЅЕїЧјМфЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯп![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉЃЌДг
ЃЉЃЌДг![]() ЩЯЕФЕу
ЩЯЕФЕу![]() зї
зї![]() жсЕФДЙЯпЃЌНЛ
жсЕФДЙЯпЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌдйДгЕу
ЃЌдйДгЕу![]() зї
зї![]() жсЕФДЙЯпЃЌНЛ
жсЕФДЙЯпЃЌНЛ![]() гкЕу
гкЕу![]() .Щш
.Щш![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() .
.
ЃЈЂёЃЉЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉМЧ![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК 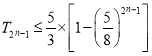 ЃЛ
ЃЛ
ЃЈЂѓЃЉШєвбжЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЌМЧЪ§Са
ЃЉЃЌМЧЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЪдБШНЯ
ЃЌЪдБШНЯ![]() гы
гы![]() ЕФДѓаЁ.
ЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABCжаЃЌB= ![]() ЃЌAC=2
ЃЌAC=2 ![]() ЃЌcosC=
ЃЌcosC= ![]() ЃЎ
ЃЎ 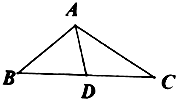
ЃЈ1ЃЉЧѓsinЁЯBACЕФжЕМАBCЕФГЄЖШЃЛ
ЃЈ2ЃЉЩшBCЕФжаЕуЮЊDЃЌЧѓжаЯпADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com