
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的离心率为
的离心率为![]() ,双曲线
,双曲线![]() 的渐近线与椭圆
的渐近线与椭圆![]() 的交点到原点的距离均为
的交点到原点的距离均为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 三点共线,直线
三点共线,直线![]() 的斜率分别为
的斜率分别为![]() .
.
(i)证明:![]() ;
;
(ii)若![]() ,设直线
,设直线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() ,证明:
,证明:![]() 为定值.
为定值.
【答案】(1)![]() (2)(i)证明见解析;(ii)证明见解析;
(2)(i)证明见解析;(ii)证明见解析;
【解析】
(1)设渐近线与椭圆![]() 交点为
交点为![]() ,根据
,根据![]() 到原点的距离和
到原点的距离和![]() 在椭圆上可得到关于
在椭圆上可得到关于![]() 的方程,结合离心率即可求得
的方程,结合离心率即可求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)由![]() 关于原点对称可假设
关于原点对称可假设![]() 坐标;
坐标;
(i)利用![]() 在椭圆上,满足椭圆方程,代入
在椭圆上,满足椭圆方程,代入![]() 中化简整理可得结论;
中化简整理可得结论;
(ii)求得![]() 后,将直线方程与椭圆方程联立得到韦达定理的形式,利用
后,将直线方程与椭圆方程联立得到韦达定理的形式,利用![]() 可得到所求定值.
可得到所求定值.
(1)设椭圆的半焦距为![]() ,由题意知:
,由题意知:![]() ,
,![]() …①,
…①,
![]() 双曲线
双曲线![]() 的渐近线方程为
的渐近线方程为![]() ,
,
![]() 可设双曲线的渐近线与椭圆
可设双曲线的渐近线与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,
,
![]() ,解得:
,解得:![]() .
.
![]() 在椭圆上,
在椭圆上,![]() ,即:
,即:![]() …②,
…②,
由①②解得:![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的标准方程为:
的标准方程为:![]() .
.
(2)由题意知:![]() 关于原点对称,则可设
关于原点对称,则可设![]() ,
,![]() ,
,![]() .
.
(i)![]() 点
点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
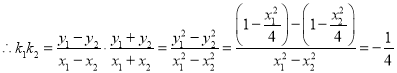 .
.
(ii)不妨设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() ,
,
![]() 直线
直线![]() ,
,![]() ,
,
由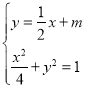 得:
得:![]() ,
,![]() ,
,
由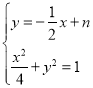 得:
得:![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
![]() 为定值
为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
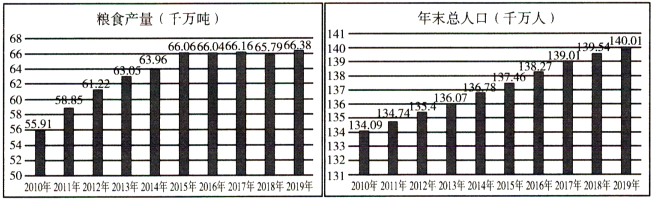
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )经过
)经过![]() ,
,![]() 两点.O为坐标原点,且
两点.O为坐标原点,且![]() 的面积为
的面积为![]() .过点
.过点![]() 且斜率为k(
且斜率为k(![]() )的直线l与椭圆C有两个不同的交点M,N,且直线
)的直线l与椭圆C有两个不同的交点M,N,且直线![]() ,
,![]() 分别与y轴交于点S,T.
分别与y轴交于点S,T.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求直线l的斜率k的取值范围;
(Ⅲ)设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中社团进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查,若开通“微博”的称为“时尚族”,否则称为“非时尚族”,通过调查分别得到如图所示统计表和各年龄段人数频率分布直方图: 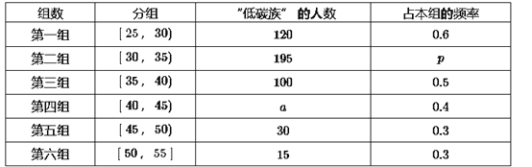
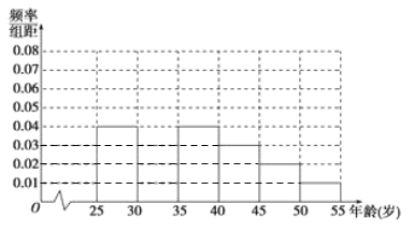
完成以下问题:
(Ⅰ)补全频率分布直方图并求n,a,p的值;
(Ⅱ)从[40,50)岁年龄段的“时尚族”中采用分层抽样法抽取18人参加网络时尚达人大赛,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X)..
查看答案和解析>>
科目:高中数学 来源: 题型:
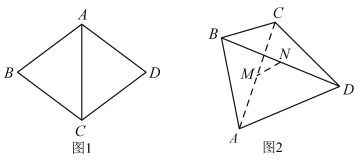
【题目】如图1.四边形![]() 是边长为10的菱形,其对角线
是边长为10的菱形,其对角线![]() ,现将
,现将![]() 沿对角线
沿对角线![]() 折起,连接
折起,连接![]() ,形成如图2的四面体
,形成如图2的四面体![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的大小为______.在图2中,设棱
所成角的大小为______.在图2中,设棱![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,若四面体
,若四面体![]() 的外接球的球心在四面体的内部,则线段
的外接球的球心在四面体的内部,则线段![]() 长度的取值范围为______.
长度的取值范围为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
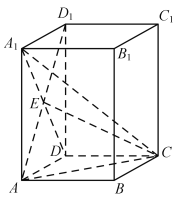
(1)证明:AE⊥平面ECD.
(2)求直线A1C与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
,直线l不过原点O且不平行于坐标轴,l与E有两个交点A,B,线段AB的中点为M.
![]() 若
若![]() ,点K在椭圆E上,
,点K在椭圆E上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
![]() 证明:直线OM的斜率与l的斜率的乘积为定值;
证明:直线OM的斜率与l的斜率的乘积为定值;
![]() 若l过点
若l过点![]() ,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
,射线OM与椭圆E交于点P,四边形OAPB能否为平行四边形?若能,求此时直线l斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
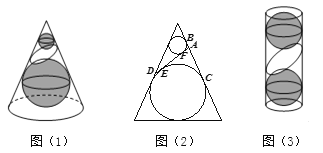
【题目】如图(1),在圆锥内放两个大小不同且不相切的球,使得它们分别与圆锥的侧面、底面相切,用与两球都相切的平面截圆锥的侧面得到截口曲线是椭圆.理由如下:如图(2),若两个球分别与截面相切于点![]() ,在得到的截口曲线上任取一点
,在得到的截口曲线上任取一点![]() ,过点
,过点![]() 作圆锥母线,分别与两球相切于点
作圆锥母线,分别与两球相切于点![]() ,由球与圆的几何性质,得
,由球与圆的几何性质,得![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,由椭圆定义知截口曲线是椭圆,切点
,由椭圆定义知截口曲线是椭圆,切点![]() 为焦点.这个结论在圆柱中也适用,如图(3),在一个高为
为焦点.这个结论在圆柱中也适用,如图(3),在一个高为![]() ,底面半径为
,底面半径为![]() 的圆柱体内放球,球与圆柱底面及侧面均相切.若一个平面与两个球均相切,则此平面截圆柱所得的截口曲线也为一个椭圆,则该椭圆的离心率为______.
的圆柱体内放球,球与圆柱底面及侧面均相切.若一个平面与两个球均相切,则此平面截圆柱所得的截口曲线也为一个椭圆,则该椭圆的离心率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com