【题目】如图，在三棱锥P-ABC中，
，
，
，
，平面
平面ABC．
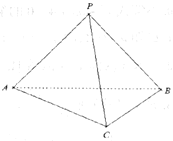
（1）求证：
平面PBC；
（2）求二面角P-AC-B的余弦值；
（3）求直线BC与平面PAC所成角的正弦值．
【答案】（1）证明见解析，（2）
，（3）
【解析】
（1）由面面垂直的性质定理可得
平面
，然后可得
，再结合条件
即可证明
（2）作
于点O，
于点M，连结
，可证明
，所以
是二面角P-AC-B的平面角，然后求出即可
（3）利用
求出点B到平面
的距离即可
（1）因为平面
平面ABC，平面
平面
，
平面
所以平面
因为
平面，所以
又因为，
所以
平面
（2）如图，作于点O，于点M，连结
因为平面平面ABC，平面平面
，
平面
所以
平面
根据三垂线定理得：
所以是二面角P-AC-B的平面角
设
，因为
所以
，
因为，
所以
，
所以
即二面角P-AC-B的余弦值为
（3）在（2）的前提下可得：
，
设点B到平面的距离为
因为
所以
所以
所以直线BC与平面PAC所成角的正弦值为
亮点激活精编提优100分大试卷系列答案科目：高中数学 来源： 题型：
【题目】荷花池中，有一只青蛙在成“品”字形的三片荷叶上跳来跳去（每次跳跃时，均从一片荷叶跳到另一片荷叶），而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图所示.假设现在青蛙在
荷叶上，则跳三次之后停在荷叶上的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
的展开式中，求：
（1）二项式系数的和；
（2）各项系数的和；
（3）奇数项的二项式系数和与偶数项的二项式系数和；
（4）奇数项系数和与偶数项系数和；
（5）
的奇次项系数和与的偶次项系数和.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
：
(
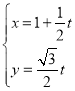为参数)，曲线
：
（
为参数）．
(1)设与相交于
两点，求
；
(2)若把曲线上各点的横坐标压缩为原来的
倍，纵坐标压缩为原来的
倍，得到曲线
，设点P是曲线上的一个动点，求它到直线的距离的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知p：x2≤5x－4，q：x2－(a＋2)x＋2a≤0.
(1)若p是真命题，求对应x的取值范围；
(2)若p是q的必要不充分条件，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知过点
作动直线
与抛物线
相交于
，
两点.
（1）当直线的斜率是
时，
，求抛物线
的方程；
（2）设，的中点是
，利用（1）中所求抛物线，试求点的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
