
已知二次函数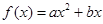 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为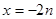 ,
,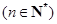 .
.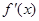 是
是 的导函数,且
的导函数,且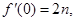
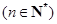 .
.
(1)求 的表达式(含有字母
的表达式(含有字母 );
);
(2)若数列 满足
满足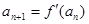 ,且
,且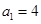 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在(2)条件下,若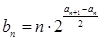 ,
,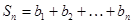 ,是否存在自然数
,是否存在自然数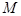 ,使得当
,使得当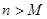 时
时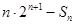
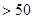 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的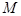 ;若不存在,说明理由.
;若不存在,说明理由.
(1)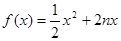 ;(2)
;(2)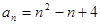 ;(3)存在自然数M=4,使得当n>M时n•2n+1-Sn>50恒成立.
;(3)存在自然数M=4,使得当n>M时n•2n+1-Sn>50恒成立.
解析试题分析:(1)利用二次函数f(x)=ax2+bx+c的图象通过原点,对称轴为x=-2n,(n∈N*).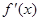 是f(x)的导函数,且
是f(x)的导函数,且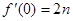 ,可求f(x)的表达式(含有字母n);
,可求f(x)的表达式(含有字母n);
(2)由(1)可得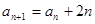 ,从而有
,从而有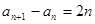 ,利用叠加法:
,利用叠加法: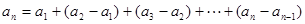 ,求出数列{an}的通项公式;
,求出数列{an}的通项公式;
(3)由(2)可知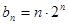 ,它是由一个等差数列
,它是由一个等差数列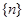 与一个等比数列
与一个等比数列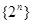 的对应项的积构成的一个新的数列,这种数列的前n项和可利用两边同时乘公比相减的错位相减法求和先求出
的对应项的积构成的一个新的数列,这种数列的前n项和可利用两边同时乘公比相减的错位相减法求和先求出 ,然后就可将不等式
,然后就可将不等式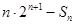
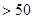 恒成立转化为只含n的不等式恒成立问题,即可得出结论.
恒成立转化为只含n的不等式恒成立问题,即可得出结论.
试题解析:(1)由已知,可得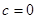 ,
,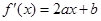 , 1分
, 1分
∴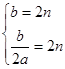 解之得
解之得 ,
,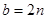 3分
3分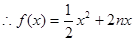 4分
4分
(2)
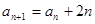 5分
5分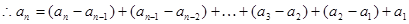
=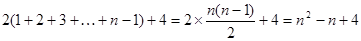 8分
8分
(3)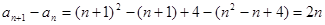
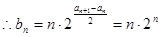 10分
10分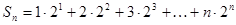 (1)
(1)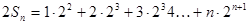 (2)
(2)
(1)—(2)得: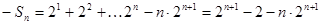 … 12分
… 12分
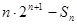 =
=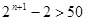 ,即
,即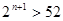 ,当
,当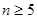 时,
时,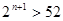 … 13分
… 13分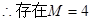 ,使得当
,使得当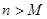 时,
时,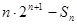
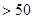 恒成立 14分
恒成立 14分
考点:1.数列的通项与求和;2.恒成立问题;3.数列与函数的综合.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)用x的代数式表示AM,并写出x的取值范围;
(2)求S关于x的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至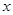 元,则本年度新增用电量
元,则本年度新增用电量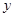 (亿千瓦时)与
(亿千瓦时)与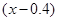 元成反比例.又当
元成反比例.又当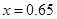 时,
时,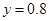 .
.
(1)求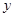 与
与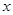 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益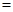 用电量
用电量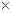 (实际电价-成本价)]
(实际电价-成本价)]
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数 与时刻
与时刻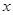 (时)的关系为
(时)的关系为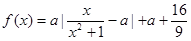 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且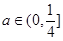 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作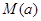 .
.
(1)令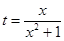 ,
, ,求
,求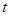 的取值范围;
的取值范围;
(2)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为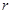 米,高为
米,高为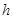 米,体积为
米,体积为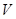 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为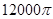 元(
元(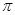 为圆周率).
为圆周率).
(1)将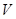 表示成
表示成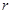 的函数
的函数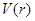 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数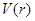 的单调性,并确定
的单调性,并确定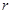 和
和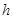 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com